|
  Imprimer Imprimer
1. Expérience
: chute d'un ensemble de ballons dans l'air.

Un élève lâche
un ensemble de 4 ballons lestés :
Volume total V = 2 2
+ 2 x 0,6 = 5,2 L et la masse total m = 22,2 g
- On filme la chute des ballons
à l'aide d'une webcam.
Réglages camera Philips
ToUcam Pro :
- video format : 320 x 240
- video source : réglage entièrement automatique
- temps : 5 secondes
- vitesse d'obturation 1/250ème de seconde
- régler le gain afin que l'image soit claire.
Données :
Masse volumique de l'air m
= 1,3 kg.m-3
Intensité de la pesanteur g = 10 m.s-2
Mise en évidence de
l'évolution de la vitesse au cours du temps :
- On pointe la position d'un
point du système (par exemple : le centre de l'un des
ballons) avec le logiciel Avimeca2.
- On calcule la vitesse des ballons à l'aide du logiciel
Regressi.
- On trace le graphe v = f(t) à l'aide
du logiciel Excel.
Les modes d'emploi de ces différents
logiciels sont donnés dans la partie TP.
On obtient le graphe suivant :
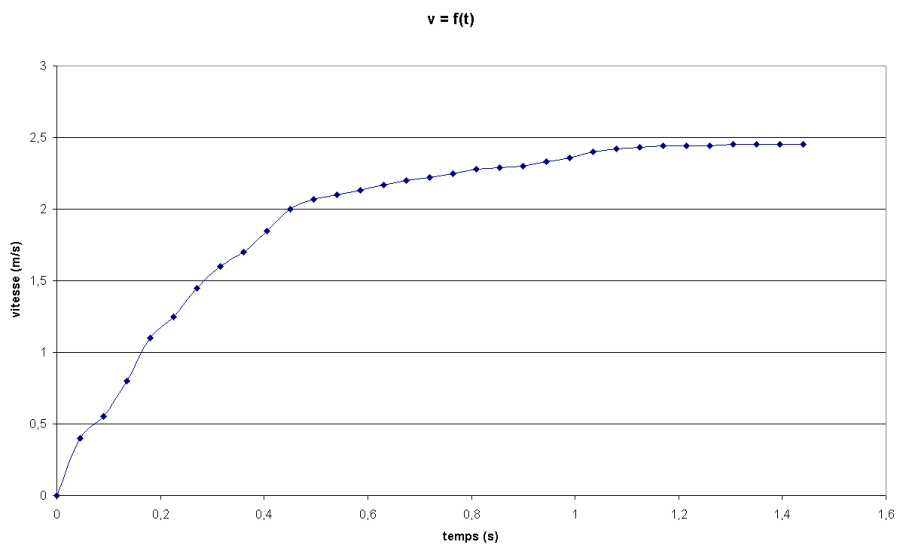
On constate que la vitesse
atteint une vitesse limite vlim = 2,45 m.s-1
Nous allons établir
deux modèles à l'aide d'équations différentielles
et discuter de la validité de ces modèles par rapport
à la courbe expérimentale trouvée ci-dessus.
2. Equations
différentielles du mouvement.
Deux équations différentielles
peuvent être établies selon l'expression des forces
de frottement
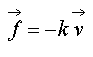 (cas d'une vitesse
faible du mobile) ou (cas d'une vitesse
faible du mobile) ou 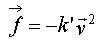 (cas
d'une vitesse élevée du mobile) (cas
d'une vitesse élevée du mobile)
Etablissement de l'équation différentielle pour
l'hypothèse :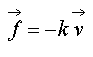
- Système : ensemble
des ballons lestés
- Référentiel : terrestre supposé galiléen
- Bilan des forces extérieures appliquées au système
:
o Poids : 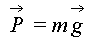
o Poussée d'Archimède : 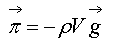
o Force de frottement fluide : 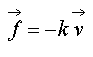
- Application de le deuxième loi de Newton :
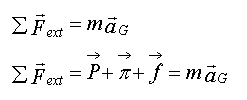
- Par projection sur l'axe
z'z
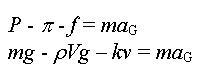
Soit :
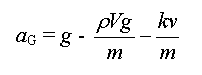
Expression de l'équation
différentielle en fonction de v et de  : :
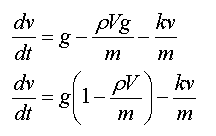
Etablissement de l'équation
différentielle pour l'hypothèse 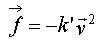 :
:
Par le même raisonnement
on obtient :
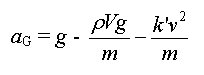
Expression de l'équation
différentielle en fonction de v et de :
:
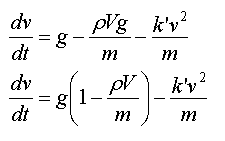
3. Résolution
de l'équation différentielle par une méthode
itérative (la méthode d'Euler).
Itérative : par répétition
Euler : Mathématicien
et physicien du 18ème siècle a qui ont doit des
travaux l'astronomie (orbites planétaires, trajectoires
des comètes), les sciences physiques (champs magnétiques,
hydrodynamique, optique, nature ondulatoire de la lumière,...),
les mathématiques, où il met au premier plan le
concept de fonction.
3.1. Résolution pour
l'hypothèse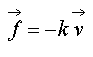
On a :
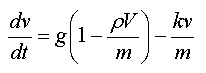
Que l'on peut écrire
sous la forme :
 ou
ou 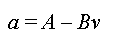
Les 3 étapes pour résoudre
cette équation :
- déterminer A
et B
- énoncer le principe de la méthode d'Euler
- appliquer la méthode d'Euler
- Détermination de A
et B
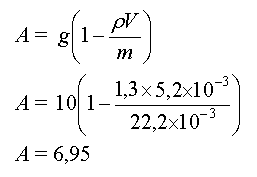
Pour trouver B, on peut
écrire que  , mais on ne connaît pas k, alors on utilise une
autre méthode :
, mais on ne connaît pas k, alors on utilise une
autre méthode :
Quand la vitesse atteint sa
valeur limite, on vlim = cste alors  =
0 =
0
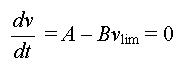
soit 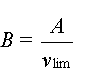
Graphiquement, on peut déterminer
la valeur de la vitesse limite vlim = 2,45
m.s-1
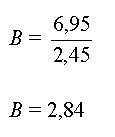
- Enoncé du principe
de la méthode d'Euler :
L'accélération varie en fonction de la vitesse
:
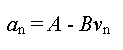
la vitesse varie en fonction
de l'accélération :
 Dt est
appelé pas du calcul.
Dt est
appelé pas du calcul.
- Application de la méthode
d'Euler :
Choix du pas de calcul :
Le pas de calcul est choisi
tel que 
Tableau de calculs itératifs :
Le remplissage des cases s'effectuent
en suivant les flèches


Etc....
Ces calculs sont évidemment
beaucoup rapides à réaliser sur un tableur.
Utilisation d'un tableur (le
mode d'emploi du tableur est vu en TP)

Graphe obtenu :

3.2. Résolution pour
l'hypothèse 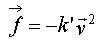
L'équation différentielle
s'écrit :
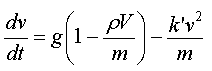
Que l'on peut écrire
sous la forme :
 ou ou 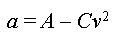
- Détermination de A
et C
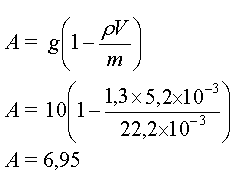
Quand la vitesse atteint sa
valeur limite, on vlim = cste alors  =
0 =
0
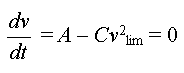
soit
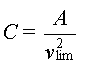
Graphiquement, on peut déterminer
la valeur de la vitesse limite vlim = 2,45
m.s-1
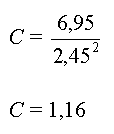
- Enoncé du principe
de la méthode d'Euler :
L'accélération varie en fonction de la vitesse
:
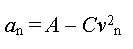
la vitesse varie en fonction
de l'accélération :
 Dt est
appelé pas du calcul.
Dt est
appelé pas du calcul.
- Application de la méthode
d'Euler :
Pas de calcul Dt = 0,02 s

Etc....
Ces calculs sont évidemment
beaucoup rapides à réaliser sur un tableur.
Utilisation d'un tableur (le
mode d'emploi du tableur est vu en TP)

Graphe obtenu :

3.3. De quel modèle,
l'expérience réalisée en classe se rapproche-telle
le plus ?
Voici représenté
sur une même feuille les 3 graphes obtenus :

- au début la courbe représentant la chute de l'expérience
se rapproche de la courbe " kv "
- au milieu, aucun modèle ne correspond au résultat
expérimental
- à la fin la courbe représentant la chute de l'expérience
se rapproche de la courbe " kv2 "
- conclusion : l'expérience réalisée n'est
pas vraiment modélisable avec les modèles proposés.
|