|
  Imprimer
Imprimer
Systèmes
oscillants
Présentation
de quelques systèmes oscillants mécaniques
I. Les oscillateurs vus
en terminale S.
Les oscillateurs étudiés
en terminale S sont :
- le pendule pesant (simple)
- le pendule élastique (voir le cours suivant)
- horizontal
- vertical (expérimentalement)
II. Le pendule simple.
1. Définitions.
Le pendule simple est un cas
particulier de pendule pesant.
1.1. Définition d'un
pendule pesant :
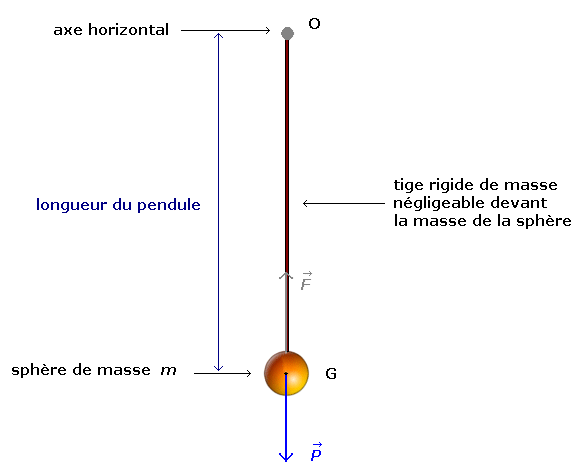
Le pendule pesant est un système
en rotation autour d'un axe horizontal.
Ecarté de sa position d'équilibre, il oscille sous
la seule action de son poids.

Question discussion réponse
Combien il y a-t-il de position
d'équilibre pour ce pendule ? Quelle est sa position d'équilibre
stable ? Pourquoi ?
Réponse :
Il y a deux positions d'équilibre.
|
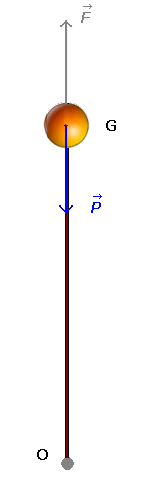
Position d'équilibre instable
car si on écarte la sphère de sa position initiale
elle ne la retrouvera jamais. |
 |
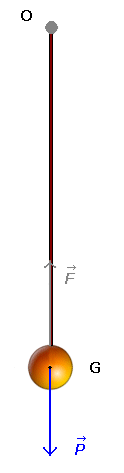 |
Position d'équilibre stable
car si on écarte la sphère de sa position initiale
elle retrouvera cette position au bout de quelques oscillations |
1.2. Définition du pendule
simple :
Le pendule simple est un pendule
pesant dont la masse m accrochée est de petite taille
par rapport à la longueur du pendule. (20 x plus petite
environ).
Le fil inextensible ou la tige rigide est de masse négligeable
devant m.
1.3. Définitions de l'écart à l'équilibre,
de l'abscisse angulaire et l'amplitude.

On décrit le mouvement
en mesurant une grandeur appelée écart à
l'équilibre stable.
Cet écart est une grandeur
angulaire notée q (t).

2. Comment
retrouver expérimentalement l'expression de la période
propre d'un pendule simple et vérifier l'isochronisme
des petites oscillations ?
Cette partie est vue en TP.
Isochronisme des petites oscillations
: pour des valeurs d'amplitude angulaire relativement faible
(qm <
20°), la période des oscillations est indépendante
de qm.
Oscillation : variation alternative
au cours du temps d'une grandeur autour de sa valeur à
l'équilibre.
Partie A : Vérification
de l'isochronisme des petites oscillations.
Remarques sur la mesure de
T

Question discussion réponse
:
Répondre par VRAI ou
FAUX en justifiant votre réponse.
- la mesure de T s'effectue
en déclenchant le chronomètre au moment où
on lâche la bille.
- la mesure de T s'effectue sur une oscillation (un aller
et retour).
Réponse :
FAUX, la mesure de T
s'effectue après une ou plusieurs oscillations afin s'affranchir
des perturbations dues au lâcher de la bille.
FAUX, le mesure de T
s'effectue sur plusieurs oscillations afin d'avoir une plus grande
précision de mesure.

Question discussion réponse
:
- Proposer une expérience
permettant de vérifier l'isochronisme des petites oscillations.
Pour cela :
- Décrire le protocole
expérimental.
- Indiquer les valeurs de :
- la masse m du solide accroché
au fil
- la longueur du pendule (fil + rayon de la bille) L
- l'amplitude choisie qm
- Réaliser cette expérience.
- Noter les résultats expérimentaux dans un tableau.
- Tracer le graphe correspondant sur un tableur.
- Conclure.
Réponse :
- Protocole expérimental
:
On choisit une valeur de m
et une valeur de L que l'on gardera constante dans toute
l'expérience.
On effectue une mesure de T pour différentes valeurs
de qm  20°. 20°.
- Valeurs choisies :
m = 100,0 g
L = 1,20 m
qm : 5 °,
10°, 15° et 20°
- On réalise l'expérience
et on trouve les résultats suivants :

- Graphe T = f (qm)

Conclusion : La période
est indépendante de l'amplitude angulaire. La loi d'isochronisme
des petites oscillations est vérifiée.
Partie B : Expression
de la période d'un pendule simple

Question discussion réponse
:
- Proposer une expérience
afin de montrer si la période dépend de la masse
m du solide accroché au fil.
- Décrire le protocole
expérimental.
- Indiquer les valeurs de :
- la longueur du pendule (fil
+ rayon de la bille) L
- l'amplitude choisie qm
- les masses m des solides
- Réaliser cette expérience.
- Noter les résultats expérimentaux dans un tableau.
- Tracer le graphe correspondant sur un tableur.
- Conclure.
Réponse :
- Protocole expérimental
:
On choisit une valeur de qm
et une valeur de L que l'on gardera constante dans toute
l'expérience.
On effectue une mesure de T pour différentes valeurs
de m.
- Valeurs choisies :
L = 1,20 m
qm = 20°
m = 50,0 g ; 100,0 g ; 150,0 g ; 200,0 g
- On réalise l'expérience
et on trouve les résultats suivants :

- Graphe T = f (m)

Conclusion : la période
du pendule simple est indépendante de la masse du solide
accroché.
Partie B : Expression de la période d'un pendule simple
(suite)

Question discussion réponse
:
- Proposer une expérience
afin de montrer si la période dépend de la longueur
L du pendule.
- Décrire le protocole
expérimental.
- Indiquer les valeurs de :
- la masse m du solide.
- l'amplitude choisie qm
- les longueurs L du pendule
- Réaliser cette expérience.
- Noter les résultats expérimentaux dans un tableau.
- Tracer le graphe correspondant sur un tableur.
- A quelle fonction mathématique, la courbe obtenue vous
fait-elle penser ?
- Réaliser un nouveau graphe afin d'obtenir une relation
de proportionnalité.
- Conclure.
Réponse :
- Protocole expérimental
:
On choisit une valeur de qm et une valeur de m que l'on
gardera constante dans toute l'expérience.
On effectue une mesure de T pour différentes valeurs
de L.
- Valeurs choisies :
qm = 20°
m = 100,0 g
- On réalise l'expérience
et on trouve les résultats suivants :

- Graphe T = f
(L)

Cette courbe ressemble à
la fonction 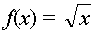
Afin d'obtenir une relation de proportionnalité, on peut
tracer le graphe T2= f (L)

Conclusion : L'expression de
la période dépend de 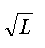
Partie B : Expression
de la période d'un pendule simple (suite)

Question discussion réponse
:
La période du pendule
dépend sans doute d'une autre grandeur, mais laquelle
?
L'analyse dimensionnelle permet
de définir la nature de cette grandeur.
On note [T] la dimension
de la période et [L] la dimension de la longueur
du pendule.
A partir des résultats
précédents, on peut écrire :
[T] = [L]1/2.
[X]a
[X] étant la
dimension de la grandeur à déterminer.
- Résoudre cette équation
aux dimensions en déterminant la dimension de [X]
en fonction [T] et [L].
- En déduire la nature de cette grandeur.
- En déduire la nouvelle expression de la période.
Réponses :
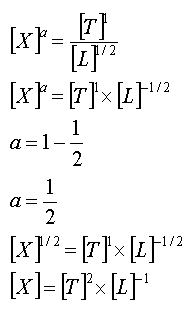
Cette grandeur est équivalente
à l'inverse d'une accélération. [a]
= [L].[T]-2
La seule accélération que subit le pendule est
l'accélération de la pesanteur.
L'expression de la période peut maintenant s'écrire
:
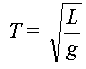
Partie B : Expression
de la période d'un pendule simple (suite)

Question discussion réponse
:
Nous allons vérifier
si la nouvelle expression de la période est validée
par les résultats expérimentaux.
- Calculer la valeur de T
pour L = 1,00 m et g = 10 m.s-2
- Si le résultat ne correspond pas aux résultats
expérimentaux, trouver la valeur de k tel que  afin d'obtenir une égalité entre les deux résultats.
afin d'obtenir une égalité entre les deux résultats.
- En déduire l'expression définitive de la période
en fonction de L, g et p
Réponse :
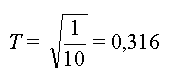
La valeur expérimentale est 2,00 s
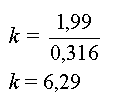
On remarque que k =
2p
Alors l'expression définitive
la période est :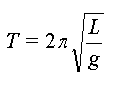
3. Amortissement
des oscillations.
On étudie le cas d'amortissements
faibles des oscillations du pendule.
Ces amortissements sont dues
aux forces de frottements fluide (air) et solide (friction sur
l'axe).

Question discussion réponse
La pseudo-période T
des oscillations faiblement amorties est-elle égale à
la période propre T0 ?
On fait osciller un pendule simple de longueur L = 25,0
cm.
On prendra g = 10 m.s-2
On obtient l'enregistrement
suivant de son amplitude angulaire. Comparer T et T0

Réponse :
Sur le graphique, on peut lire
la pseudo-période.
On prend 3 oscillations.
On mesure 3T = 3,0 s
Alors la pseudo-période
est égale à T = 1,0 s
Par le calcul, on détermine
la valeur de la période propre.
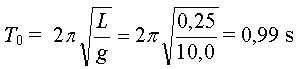
Conclusion : T0  T pour des amortissements faibles la pseudo-période
T est voisine la période propre T0.
T pour des amortissements faibles la pseudo-période
T est voisine la période propre T0.
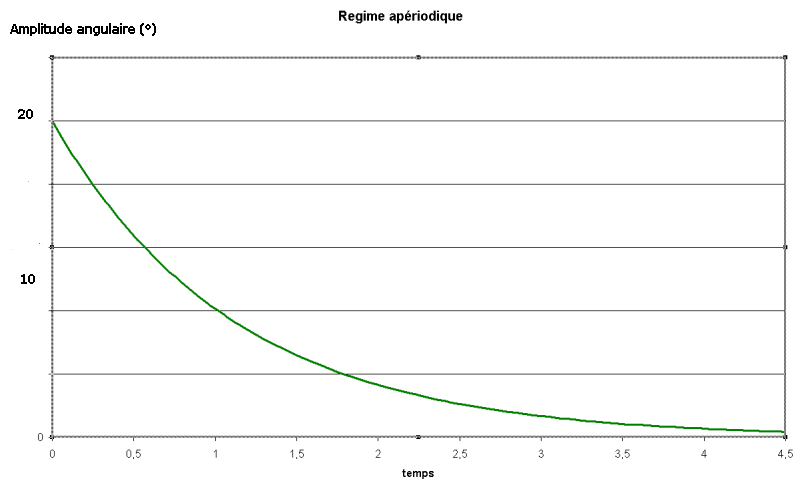
Si les amortissements étaient
beaucoup plus élevés, on obtiendrait un régime
apériodique.
 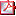 Imprimer
Imprimer
Le dispositif solide-ressort
I. Force de rappel exercée
par un ressort.
Les ressorts étudiés
sont des ressorts à spires non jointives, c'est à
dire qu'ils peuvent être comprimés ou étirés.
On note la force de rappel
exercée par un ressort.
Les caractéristiques
de la force de rappel  d'un
ressort sont : d'un
ressort sont :
- direction : celle du ressort
- sens : vers la position d'équilibre
- intensité : F = k | l - l0
| = k| x |
k est la raideur du ressort (N.m-1)
l0 est la longueur du ressort au repos
x est l'allongement
Afin d'établir l'expression
vectorielle de la force de rappel d'un ressort, nous allons étuidiés
les deux cas de figures suivants :
Compression :

- x < 0
-  dans
le sens de dans
le sens de 
Alors car -kx > 0 ( est
bien dans le sens de est
bien dans le sens de  ) )
Allongement :

- x > 0
-  dans
le sens opposé à dans
le sens opposé à
Alors car -kx < 0 (  est
bien dans le sens opposé à est
bien dans le sens opposé à  ) )
II. Etude dynamique du système
" solide ".
1. Oscillation
d'un solide soumis à l'action de deux ressorts horizontaux.
2. Etablissement
de l'équation différentielle du mouvement.
- Système : le solide
accroché au ressort.
- Référentiel : terrestre supposé galiléen
- Bilan des forces :
§ le poids 
§ la réaction normale au plan 
§ la force de rappel du ressort 
§ la force de frottement 
m étant le coefficient de frottement fluide
- Application de la deuxième
loi de Newton :
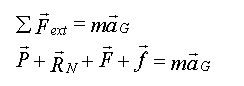
- Par projection sur l'axe

Cette équation différentielle
décrit le mouvement oscillant suivant l'axe  du
pendule élastique. du
pendule élastique.
Si les frottements sont négligeables
:

- Vérifions que  est une solution de l'équation différentielle
est une solution de l'équation différentielle 
Mais tout d'abord donnons la signification de tous les termes
de cette solution :

t étant le temps (s)
Dans un premier temps, calculons  et et


donc

L'équation différentielle
est bien vérifiée.
3. Période
des oscillations.
On note T0
la période propre des oscillations
L'expression de la solution
de l'équation différentielle peut s'écrire
sous deux formes :

Par comparaison, on a :

Alors

4. Vérification
de l'homogénéité de l'expression de la période
propre par analyse dimensionnelle.

Sachant que :
- l'expression de la force de rappel d'un ressort est F
= k | l - l0 | = k| x |
- la deuxième loi de Newton s'écrit dans ce cas
F = maG
On obtient :
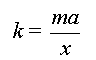
Donc 

 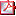 Imprimer
Imprimer
Le phénomène
de résonance
I. Exemples spectaculaires
de résonances mécaniques.
1. Destruction
du pont de Tacoma.
Regarder la vidéo suivante
:

1,2 Mo |
 Source : itnsource.com (Pathe Gazettes / Pathe Newsreels)
Source : itnsource.com (Pathe Gazettes / Pathe Newsreels) |
Le 7 novembre 1940, des voitures
traversent le pont de Tacoma.
Des rafales de vent violentes et périodiques frappent
le pont.
Le pont commence à osciller et se rompt !
Mais pourquoi ? Nous allons
répondre à cette question dans la suite du cours.
2. Le pont
suspendu de Basse-Chaîne à Angers.

Le 16 avril 1850, Le 3ème
bataillon du 2ème léger se rend à Angers
pour une revue.
Une tempête balaye Angers, les soldats têtes baissées
marchent sur le pont.
Brutalement, quand une partie du bataillon atteint la rive gauche,
le pont se rompt ! 226 morts !
Mais pourquoi ? Nous allons
répondre à cette question dans la suite du cours.
II. Présentation
expérimentale du phénomène de résonance.
Cette partie peut être
vue en TP.

Le dispositif est constitué
de deux pendules reliés entre-eux par un ressort.
On met en mouvement le pendule
appelé excitateur.
Le pendule appelé résonateur
se met en mouvement.
Les oscillations sont dites " forcées "
Vous pouvez observer ces oscillations
dans la vidéo suivante :

11 Mo |
 |

Questions discussion réponse
II.1. Détermination
de la période propre du résonateur. (Etude d'un
document).
Le document suivant a été
réalisé en pointant sur une vidéo des oscillations
du résonateur, la position du centre du disque fixé
à la tige.
Les conditions du pointage
sont décrites sur le schéma suivant :


Remarque (hors programme) :
le mouvement irrégulier obtenu (augmentation puis diminution
de l'amplitude des oscillations et ainsi de suite) est dû
au fait que le résonateur reçoit des impulsions
qui ne sont plus synchrones avec sa période propre. Tantôt,
il est en concordance, tantôt il est en discordance avec
son propre mouvement oscillatoire. Ces alternances de mouvement
maximum et de repos constituent un cas particulier du phénomène
des battements (superposition de deux phénomènes
vibratoires de type interférence). Ce n'est pas le
phénomène de résonance.

Déterminer la période propre du résonateur
; Indiquez votre méthode. T0 = …………
s
Réponse :
Afin de déterminer la
période propre du résonateur, on mesure la durée
nécessaire afin d'effecteur 10 oscillations.
 
L'origine des axes étant situé à la position
d'équilibre du pendule, une oscillation
(un aller et retour) correspond sur le graphique à la
durée pour passer d'un maximum
au 2ème maximum.
On trouve 10 T0
= 11,5 s
Valeur de la période
propre du résonateur T0 = 1,15 s
II.2. Comment
faire varier la période de l'excitateur ?

1. En utilisant le dispositif
proposé, donner une méthode afin de faire varier
la période de l'excitateur.
2. On détermine expérimentalement
les valeurs extrêmes des périodes de l'excitateur.
…………….
< T < ………………
Réponse :
Le dispositif permet de faire
varier le centre d'inertie de la tige de l'excitateur en déplaçant
le contre-poids du pendule excitateur.
(En simplifiant , on peut assimiler ce déplacement à
la variation de longueur d'un pendule simple)
1,12 s < T < 1,20
s
II.3. Evolution
de l'amplitude du résonateur en fonction de la période
de l'excitateur.
1. On réalise les mesures
d'amplitude et on complète le tableau suivant :
d : distance entre l'axe et le haut du contre-poids.

Résultats :

2. On trace le graphe Amplitude = f (d)


On a montré que la période
T dépendait de la distance d.
- L'amplitude du résonateur
dépend-elle de la période de l'excitateur T
?
- Pour quelle valeur de d a-t-on l'amplitude la plus élevée
?
Réponse :
- L'amplitude du résonateur
dépend de la période de l'excitateur.
- Pour d = 27,0 cm on obtient la valeur maximale de l'amplitude
de résonance.
3. Détermination expérimentale
de la période de l'excitateur quand l'amplitude est maximale.
- On effectue la mesure de
10 périodes quand l'amplitude est maximale. 10 T
= ………..
- On détermine la période
T correspondante. T = …………
Réponse :
10 T = 11,5 s et T
= 1,15 s
4. Bilan des différentes
expériences.

- Comparer la valeur de la
période du résonateur (déterminée
dans la partie I) avec celle de l'excitateur qui permet d'obtenir
l'amplitude maximale.
- Conclusion ?
Réponse :
- La valeur du résonateur
est égale à 1,15 s
- La valeur de la période de l'excitateur permettant d'obtenir
une amplitude maximale est 1,15 s.
- Conclusion : Quand la période T de l'excitateur est
voisine de la période propre du résonateur, on
a un phénomène de résonance.
III. Influence de l'amortissement.
T0 est la
période propre du résonateur.
On utilise le dispositif soumis à trois situations différentes
:
o pas de frottements
o quelques frottements
o beaucoup de frottements
On fait varier la fréquence
de l'excitateur comme dans l'expérience précédente.


Question discussion réponse
L'existence de frottements
modifie-t-elle :
o l'amplitude maximale à
la résonance ?
o la fréquence (ou la période) de résonance
?
Réponse :
o l'amplitude maximale à
la résonance diminue quand les frottements augmentent.
o La fréquence de résonance est indépendante
de l'existence de frottements.
IV. Pourquoi les ponts de
Tacoma et d'Angers sont-ils rentré en résonance
? (Bilan)

Question discussion réponse
A partir des éléments
de cours précédents, proposer une explication aux
phénomènes observés sur ces deux ponts.
Les rafales de vent ont une
période T ou fréquence f. Elles constituent
l'excitateur.
Les ponts dont la structure est oscillante ont une période
propre T0 ou fréquence propre f0.
Ils constituent le résonateur.
Quand la fréquence des rafales a atteint la valeur de
la fréquence propre des ponts, ils sont entré en
résonance.
On peut observer ces phénomènes
de résonance dans d'autres dispositifs, comme les instruments
de musique à vents ( trompette, orgues) ou les instruments
à cordes avec une caisse de résonance (guitare). |