Imprimer

I. Un exemple d'application d'un circuit RL : un composant du système d'alimentation en gazole d'une Logan.

Extrait de l'introduction du sujet LIBAN 2006

La Dacia Logan, conçue par le constructeur français Renault est produite au départ en Roumanie.
Elle a fait la une de l'actualité lors de son lancement commercial : elle était en effet présentée comme " la voiture à 5000 euros ". Même si son prix fut finalement plus élevé que prévu, les journalistes automobiles étaient impatients d'évaluer cette voiture d'un nouveau genre.
L'exercice propose d'étudier un composant du système d'alimentation en gazole du moteur Diesel qui peut équiper la Logan.

Malgré les tarifs modérés de la Logan, son moteur Diesel bénéficie d'une technologie de pointe : le système d'injection directe de gazole par rampe commune. L'élément essentiel est l'injecteur qui pulvérise en quelques fractions de seconde une très faible quantité de gazole directement dans la chambre de combustion où se produit l'explosion du mélange air-gazole.
On peut schématiser cet injecteur par un long tube creux, percé à son extrémité inférieure d'un très petit trou bouché par une aiguille. C'est par ce trou que pourra sortir le gazole lorsque l'aiguille sera déplacée vers le haut.
Pour déplacer cette aiguille métallique vers le haut, on utilise une bobine qui, lorsqu'elle est traversée par un courant électrique, se comporte comme un aimant et attire alors l'aiguille à elle. Dès que le courant est coupé, l'aiguille reprend sa position initiale et bouche à nouveau le trou.

Question discussion réponse

1. Identifier la bobine dans le circuit.
2. Il y-a-t-il perte d'énergie dans cette bobine ? Pourquoi ?
3. Comment se comporte une bobine lorsqu'elle traversée par un courant électrique ?

Réponse :

1. La bobine est représentée par le symbole
2. Il y a perte d'énergie thermique par effet Joule dans la résistance.
3. La bobine se comporte comme un aimant lorsqu'elle est traversée par un courant électrique.

II. La bobine.

1. Description.

Une bobine est constituée d'un enroulement d'un fil conducteur gainé par un matériau isolant.

Exemples de formes de bobines que vous utiliserez au laboratoire :

- Représentation symbolique :
- La bobine est caractérisée par deux grandeurs physiques :

- sa résistance r (W)
- son inductance L Henry (H)

On peut représenter dans la convention récepteur la bobine ainsi :

2. Inductance L de la bobine.

Expérience vue en TP.

On réalise la simulation du montage suivant :

La résistance r de la bobine est considérée négligeable par rapport à la résistance R = 10 kW
L = 100 mH

Attention : vous remarquerez que d'insérer la masse entre les deux composants dont on veut mesurer la tension, entraîne que l'une d'entre-elles est négative.

Simulation accessible sur le site : http://www.ac-orleans-tours.fr/physique/phyel/term/bobine/index.htm#

Question discussion réponse :

- Décrivez l'allure des deux tensions mesurées.
- Quel outil mathématique permet de " passer " de la trace de la tension uR à celle de la tension uL ?
- Quelle est l'influence de la valeur de L sur les courbes obtenues.
- Quelle hypothèse peut-on faire quant à l'expression de la tension uL ?

Réponse :

- La tension uL aux bornes de la bobine est une constante positive, puis une constante négative à chaque demi-période.
La tension uR = -Ri varie selon une fonction affine décroissante puis croissante à chaque demi-période.
- La dérivée par rapport au temps, permet de passer de uR à uL .
- Si on diminue la valeur de L sur le simulateur, on diminue la valeur de uL .
- uL dépend de et de L, on peut faire alors l'hypothèse suivante quant à l'expression de uL :

L'expression de la tension aux bornes de la bobine est

L : inductance (H) (A.s^-1) uL (V)

3. Relation entre intensité et tension dans le cas d'une bobine résistive.

Une bobine sans résistance est dite pure (cas théorique)
Une bobine résistive possède une résistance r

III. Effet d'une bobine sur un courant.

1. Dispositif expérimental.

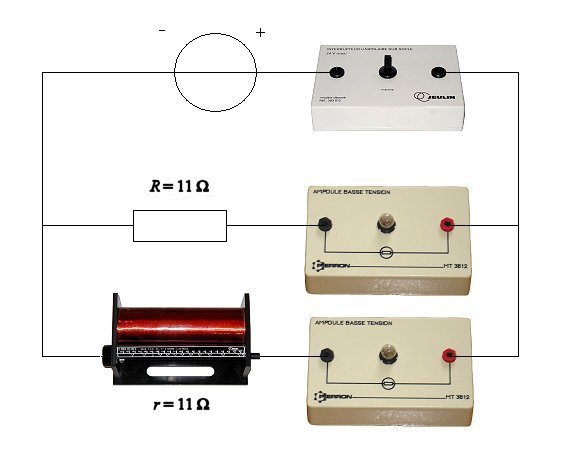
On a réalisé le montage suivant :

Question discussion réponse :

- Observez les deux lampes de chaque branche lorsqu'on établit le courant. Que remarquez-vous ?
- Quelle hypothèse pouvez-vous sur l'influence de la bobine sur l'établissement du courant ?
- L'intensité subit-elle une discontinuité dans la branche de la lampe ?
- L'intensité subit-elle une discontinuité dans la branche de la bobine ?

Observation :

Réponses :

- On remarque que la lampe située dans la branche comprenant la bobine s'allume en retard par rapport à celle de l'autre branche.
- On peut formuler l'hypothèse suivante : La bobine retarde l'établissement du courant.
- Oui, il y a discontinuité dans la branche de la lampe. Le transfert d'énergie du générateur à la lampe est instantané.
- Non, il n'y a pas discontinuité dans la branche de la lampe. Le transfert d'énergie du générateur à la bobine n'est pas instantané.

La bobine s'oppose aux variations de l'intensité du courant dans le circuit où elle se trouve.

IV. Résolution analytique pour l'intensité du courant dans un dipôle RL.

L'étude expérimentale est réalisée en TP

1. Etablissement de l'équation différentielle.

Le générateur fournit une tension en créneau (u = 0 puis u = E et ainsi de suite prériodiquement)

On applique la loi d'additivité des tensions :

2. Solution de l'équation différentielle.

Vérifions que est une solution de l'équation différentielle.
t, A et B sont des constantes à déterminer.

Dans un premier temps, on dérive Rappel :

Dans un deuxième temps, on reporte i et dans l'expression

Dans un troisième temps, on identifie A et t.

Pour que l'équation différentielle soit vérifiée à tout instant, il faut s'affranchir du temps, c'est à dire éliminer le terme qui dépend du temps :

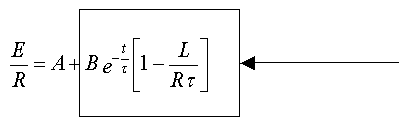ce terme

Dans un quatrième temps, on identifie B.

On prend en compte les conditions initiales à t = 0.

à t = 0 i = 0

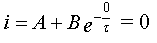
Soit A + B = 0 car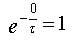

Donc B = -A

La solution de l'équation différentielle s'écrit alors :

3. Réponse en tension d'une bobine.

Question discussion réponse :

Trouver l'expression de la tension uL en utilisant la relation

Réponse :

en remplaçant la constante de temps par son expression

V. Vérification de l'unité de la constante de temps par analyse dimensionnelle.

Quelle est la dimension de ?

- D'après la loi d'Ohm, u = Ri soit

La dimension de R s'écrit (1)

- A partir de l'expression
La dimension de

La dimension de après simplification

La constante de temps a la dimension d'un temps.

Son unité est la seconde (s).

Attention : Si on tient compte de la résistance r de la bobine en plus de la résistance R, l'expression de la constante de temps devient

VI. Influence de R et de L lors de l'établissement du courant. Détermination expérimentale de t.

Cette partie est vue expérimentalement en TP.

VII. Energie emmagasinée dans une bobine.

Une bobine d'inductance L traversée par un courant d'intensité i emmagasine de l'énergie magnétique dont l'expression est :

E s'exprime en Joules (J) L (H) et i (A)