|
  Imprimer Imprimer
Extrait de l'examane
"Borgs"
Circuit RLC
Simulation
d'une transmission Borg.
Afin d'interférer avec
les signaux que les Borgs émettent et ainsi prendre un
avantage certain
lors de futurs affrontements, Jean-Luc Picard propose à
DATA de réaliser une simulation
électrique de ce signal sinusoïdale.
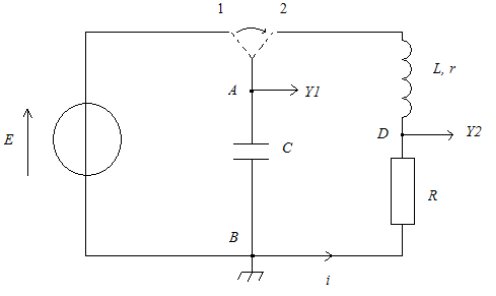
DATA réalise le circuit
suivant :
Il charge au préalable
le condensateur
sous la tension E, puis il bascule
l'interrupteur en position 2.
cet à ce moment que commence son
expérience.
Données :
E = 4,5 V R variable
r = 14 W C variable
L variable
1. Quelle grandeur est visualisée
sur le voie 1 ?
2. Quelle grandeur est visualisée sur le voie 2 ?
3. DATA se place dans le cas idéal où la résistance
totale de la branche comportant
la bobine est nulle.
a. Etablir l'équation différentielle vérifiée
par la charge q portée par l'armature A du condensateur.
b. En déduire l'équation différentielle
vérifiée par la tension uC aux bornes du condensateur.
c. Vérifier qu'une solution de cette équation différentielle
est de la forme 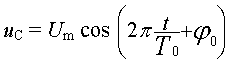
Um, T0 et f0
étant des constantes à déterminer.
4. DATA qui essaye souvent
d'amuser l'équipage de l'Enterprise, vous propose un jeu
simple ;
complétez une nouvelle
démonstration pour établir l'équation différentielle
vérifiée par la charge q,
toujours en considérant la résistance totale de
la branche comportant la bobine est nulle
Vous présenterez vos
réponses sous la forme :
(1) : ………………
(2) : ………………
A chaque instant, l'énergie
totale Em du circuit est égale à la somme des énergies
stockées dans
le condensateur et la bobine.
L'expression de l'énergie
stockée dans le condensateur a pour expression Ec
= …(1)…
L'expression de l'énergie stockée dans la bobine
a pour expression EL = …(2)…
La somme des énergies
stockées dans le condensateur et la bobine étant
constante à tout instant,
on peut écrire que 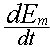 =…(3)…
alors =…(3)…
alors 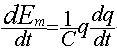 +…(4)
…= (3) +…(4)
…= (3)
donc 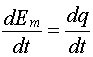 =
(3) =
(3)
ainsi l'équation différentielle
est …(6)…= (3)
III. Test en
conditions réelles du circuit réalisé par
DATA.
Dans la pratique, la résistance
totale de la branche comportant la bobine n'est pas négligeable.
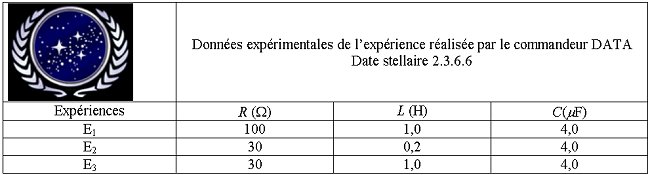
DATA réalise trois expériences afin d'étudier
l'influence des différents paramètres sur les oscillations.
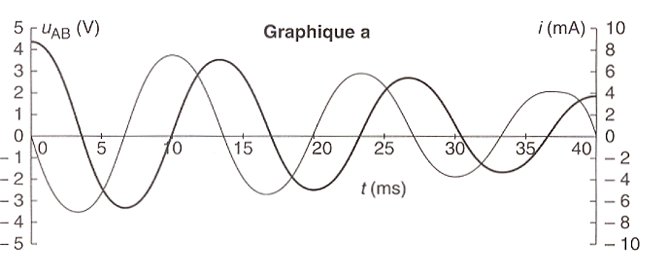
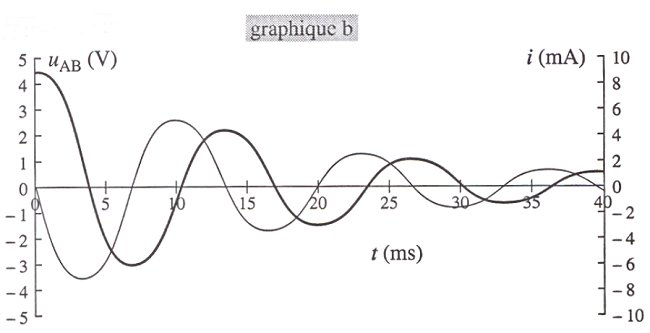
Les graphiques a, b, et c (ci-dessous) représentent les
variations de la tension uAB et de l'intensité du courant
dans le circuit.
Pour les trois graphiques :
la courbe en trait épais correspond à la tension,
celle en trait fin à l'intensité.
1. Calculer les périodes propres T01, T02,
T03 correspondant à chaque expérience
E1, E2, E3.
2. Mesurer graphiquement la période des oscillations sur
les graphiques a, b, et c
(il s'agit en fait de pseudo-période que l'on pourra confondre
avec la période propre).
3. Faire correspondre chaque graphique a, b, et c à une
des trois expériences E1, E2, E3 en le justifiant à
partir des données des graphiques.

 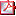 Imprimer Imprimer
Correction de l'extrait
de l'examen "Borgs"
Circuit RLC
II.1. On visualise la tension
aux bornes du condensateur. 0,25 point
II.2. On visualise la tension
aux bornes de la résistance c'est à dire l'intensité
du courant car on a
uR = Ri. 0,25 point
II.3.a. On applique la loi d'additivité des tensions :
uL + uC = 0 alors  avec i = dq / dt 0,5 point
avec i = dq / dt 0,5 point
II.3.b. L'équation différentielle vérifiée
par uC est :  avec q = Cuc 0,5 point
avec q = Cuc 0,5 point
II.3.c. Vérifions que  est bien une solution de l'équation différentielle.
est bien une solution de l'équation différentielle.
Dans un premier temps, dérivons deux fois uC ,
alors 
Dans un second temps, remplaçons
dans l'équation différentielle les expressions
de uC et de  :
:
 0,25 point
0,25 point
Factorisons

Dans un troisième temps, déterminons l'expression
de T0. A tout instant cette équation est vérifiée
si 
Alors 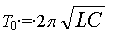 0,25 point
0,25 point
Dans un quatrième temps,
déterminons Um et f0
en se plaçant dans les conditions initiales.
A t = 0 on a  = 0
= 0
alors uc = Um.
et f0 = 0 0,25 point
Alors 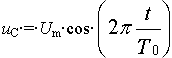
II.4. (1) =  (2)
= (2)
=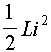 (3) = 0 (4) =
(3) = 0 (4) =  (5)
= (5)
= 0,75 point
0,75 point
(6) =
III.1.  =
12,6 x 10-3 s = 12,3 ms =
12,6 x 10-3 s = 12,3 ms
 = 5,6 x 10-3 s = 5,6 ms 0,75 point
= 5,6 x 10-3 s = 5,6 ms 0,75 point
III.2. On détermine
les périodes propres par mesure de la durée entre
2 pics et on divise par 2.
On trouve : T01 = T02 = 13 ms et T03 = 6
ms. 0,75 point
III.3. Dans les expériences
E1 et E3 les valeurs de L et de C sont les mêmes, alors
la période est la même,
ils s'agit donc des graphiques a et b. De plus le graphique b
est plus amortie alors il s'agit de
l'expérience 1
car la résistance est plus élevée.
Graphique a : E3
Graphique b : E1
Graphique c : E2 0,75 point |