|
  Imprimer Imprimer
I. LES ONDES SISMIQUES (AFRIQUE
JUIN 2003) ETUDE D'UN SEISME
Lors d'un séisme, la Terre est mise en mouvement par des
ondes de différentes natures, qui occasionnent des secousses
plus ou moins violentes et destructrices en surface. On distingue
:
- les ondes P les plus rapides,
se propageant dans les solides et les liquides.
- les ondes S, moins rapides, ne se propageant que dans les solides.
L'enregistrement de ces ondes par des sismographes à la
surface de la Terre permet de déterminer l' épicentre
du séisme (lieu de naissance de la perturbation).
Les schémas A et B modélisent
la progression des ondes sismiques dans une couche terrestre.
1. Les ondes P appelées aussi ondes de compression, sont
des ondes longitudinales.
Les ondes S, appelées aussi ondes de cisaillement, sont
des ondes transversales.
a) Définir une onde
transversale.
b) Indiquer le schéma correspondant à chaque type
d'onde.

2. Un séisme s'est produit
à San Francisco (Californie) en 1989.
Le document ci-dessous présente
le sismogramme obtenu, lors de ce séisme à la station
Eureka.
Le sismogramme a été enregistré à
Eureka, station sismique située au nord de la Californie.
L'origine du repère (t= 0 s) a été choisie
à la date du début du séisme à San
Francisco.

Le sismogramme présente
deux trains d'ondes repérés par A et B.
a) À quel type d'onde
(S ou P) correspond chaque train ? Justifier votre réponse
à l' aide du texte d'introduction.
b) Sachant que le début du séisme a été
détecté à Eureka à 8 h 15 min 20
s TU (Temps Universel), déterminer l'heure TU (h; min;
s) à laquelle le séisme s'est déclenché
à l'épicentre.
c) Sachant que les ondes p se propagent à une célérité
moyenne de 10 km .s-1, calculer la distance séparant
l'épicentre du séisme de la station Eureka.
d) Calculer la célérité moyenne des ondes
S.
II. DETERMINATION DE LA CELERITE DU SON DANS L'AIR.
1. Décrire à
l'aide d'un schéma légendé le dispositif
expérimental permettant de déterminer la célérité
du son dans l'air à partir un signal sonore continu. Vous
indiquerez le principe de l'expérience.
2. Résultats expérimentaux.
Les conditions expérimentales
sont :
Fréquence du signal
: f = 3 300 Hz
Célérité du son dans l'air : v = 330 m.s-1
Position du microphone 1 par rapport à la source sonore
: d = 12 cm.
Tension aux bornes du microphone 1, mesurée sur la voie
1 : U1 = 6 V.
Touche DUAL enfoncée.
Calibre : 2 V.div-1
Base de temps : 100 ms.div-1
2.1 Pour quelles positions
du microphone 2 par rapport à la source, observera-t-on
des signaux en phase ?
(intervalle de mesure : 0 à 50 cm en partant de la source
sonore)
2.2. Dessiner l'oscillogramme
des deux courbes obtenues si le microphone 2 est située
à une distance d' = 17 cm de la source sonore.
(Vous dessinerez une amplitude, pour le microphone 2, approximative
mais cohérente avec les données du texte)

  Imprimer Imprimer
Correction de IE1
ondes
I. Les ondes sismiques.
1.a. Définition de l'onde
transversale (voir cours). 1 pt
1.b. Schéma A : ondes longitudinales (direction du mouvement
des éléments parallèle à la
direction de propagation de l'onde). 1 pt
Schéma B : ondes transversales (voir définition).
2.a.Dans l'énoncé
on peut lire, " les ondes P sont plus rapides ". Les
premières ondes ont été
enregistrées à la date 40 s. Il s'agit du train
d'ondes A.
Alors Ondes P : train d'ondes A 2 pts
Ondes S : train d'ondes B
2.b.Le séisme s'est
déclenché à l'épicentre à
la date t = 8 h 15 min 20 s - 40 s = 8 h 14 min 40 s 1pt
2.c. La distance à l'épicentre
est d = c.Dt = 10 x 40 = 400 km 1 pt
2.d. La célérité
moyenne des ondes S est 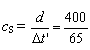 = 6,15 km.s-11 pt
= 6,15 km.s-11 pt
II. Célérité
du son dans l'air.
1. Schéma légendé
(voir cours). 2 pts
Principe :
· un signal sonore continu est émis par un haut-parleur
alimenté par un
générateur basse fréquence.
· Ce signal est reçu par un premier microphone
relié à la voie 1 d'un oscilloscope
et par un second microphone relié à la voie 2 de
l'oscilloscope, mais placé plus
loin de la source. 2 pts
· On déplace le second microphone par rapport au
premier afin de trouver les
positions auxquelles, les signaux reçus sont en phase.
· La distance entre deux situations de mise en phase est
appelée longueur d'onde.
(Période spatiale).
2.1. Afin de déterminer
les positions relatives entre les deux microphones pour lesquelles
les signaux
sont en phase, on calcule dans un premier temps la longueur d'onde
du signal.
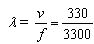 = 0,1 m 2 pts = 0,1 m 2 pts
Les positions du microphone 2 seront :
· 12 - 10 = 2 cm
· 12 + 10 = 22 cm
· 12 + 2 10 = 32 cm 2 pts
· 12 + 3 10 = 42 cm
2.2 A la distance d' = 17 cm,
on se situe à une demi-longueur d'onde. Les signaux seront
donc
en opposition de phase. 1 pt
La tension en voie 1 est de
6 V, soit 6/2 = 3 divisions 0,5 pt
La période est égale à 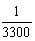 =
3 x 10-4 s = 300 ms, soit =
3 x 10-4 s = 300 ms, soit 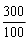 = 3 divisions. 0,5 pt
= 3 divisions. 0,5 pt
La période du second
signal est la même que le premier, par contre son amplitude
sera plus
faible.(L'intensité sonore par unité de surface
reçue par le microphone 2 est plus faible). 1 pt
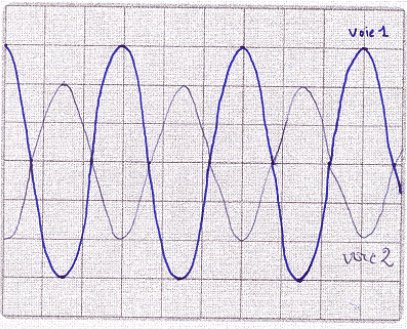 2 pts
2 pts
  Imprimer Imprimer
Exercice II du DST
de janvier 2006
Exercice II : Quelques aventures
ardéchoises 5,5 points
Lors d'un voyage scolaire organisé
par leur professeur d'EPS en Ardèche, les élèves
vécurent des aventures palpitantes. En voici, quelques
unes.
I. Le grand
plongeon.
Lors d'une descente en canyoning,
l'un des jeunes aventuriers que l'on appellera MG, décide
de sauter d'une hauteur h = 8 m dans le torrent du Chassezac.
En-dessous de lui à la verticale, nage un autre aventurier
que l'on appellera GF.
MG prévient son camarade GF à la date t0
= 13 h 31 min 24 s qu'il saute maintenant en emettant un son
de fréquence f = 400 Hz.
1. Etablir la relation entre
la célérité du son v, la hauteur
h, la date t d'arrivée du son jusqu'à
GF et la date t0.
2. Déterminer la date d'arrivée du signal sachant
que la célérité du son est v = 340 m.s-1.
3. L'onde sonore est-elle transversale ou longitudinale ? Justifier.
4. Quelle est la longueur d'onde
l du son émis par
MG ?
5. GF prévenu, nage pour s'éloigner du point de
chute de MG. Il nage à la vitesse constante v =
1,2 m.s-1. Au moment où GF commence à s'éloigner,
MG saute et arrive 1,26 s plus tard. A cet instant GF arrête
de nager. MG crée une vague qui rattrape GF au bout de
7,2 s.
Quel est la vitesse de l'onde à la surface de l'eau ?
6. L'onde à la surface de l'eau est-elle une onde transversale
ou longitudinale ? Justifier.
7. Cette onde déplacera-t-elle GF ? Si oui dans quelle
direction ?
II. Une
autre aventure : le barbotage au bord de la piscine.
Assise au bord de la piscine en attendant ses professeurs PR
et PM, CM bat du pied dans l'eau, régulièrement
à la fréquence f = 2,0 Hz et crée ainsi
une onde périodique à la surface de l'eau de hauteur
maximale 0,15 m.
Le déplacement des éléments du milieu peut
être décrite par l'équation suivante : 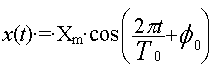
1. Que représente Xm, et f0 ?
2. En prenant f0 = 0, déterminer l'expression
de la vitesse de l'onde v(t).
3. Quelle est la hauteur de la vague à la date t0 =
0 ?
4. Quelle est la hauteur de la vague à la date t
= 4,0 s
5. Donner les dates comprises entre [0 ; 1 s] auxquelles la hauteur
de la vague est nulle.
6. Déterminer la vitesse du déplacement des éléments
du milieu à la date t = 1,0 s.
7. Déterminer la vitesse du déplacement des éléments
du milieu à la date t = 0,125 s.
III. Voyage
au centre de la Terre.
Les élèves ont découvert la spéléologie
en s'enfonçant dans des boyaux étroits, sombres
et humides.
Après le fameux passage des Egyptiens (nommé ainsi
car on ne peut passer que de profil), ils arrivent dans une salle
1 reliée à une autre salle 2 par une ouverture
de largeur a.
1. Un élève que
l'on appellera PPJ, situé dans un salle 1, lance un cri
d'effroi continu de fréquence
f = 340 Hz au moment où sa lampe à acétylène
s'est éteinte.
On a représenté sur la figure suivante, le début
de la propagation de l'onde sonore à partir de PPJ par
des cercles concentriques. (on s'est limité à la
représentation des ondes dans un plan horizontal). Un
trait peut par exemple relier les points où une compression
en phase de l'air est observée.
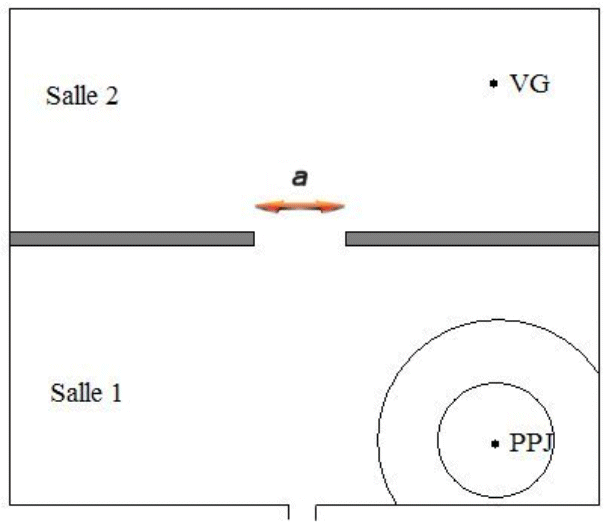
Déterminer la valeur
de la longueur d'onde de cette onde sonore, en déduire
l'échelle utilisée dans la figure ci-dessus.
Rappel : c = 340 m.s-1
2. L'onde sonore arrive au niveau de l'ouverture de largeur a
et subit le phénomène de diffraction.
2.1. Représenter les
ondes après le passage par l'ouverture.
2.2. Quelle doit être la largeur de la fente pour que le
phénomène de diffraction ait lieu.
2.3. Si l'ouverture avait été plus grande, VG aurait-il
mieux entendu le cri de PPJ ? Justifier.
 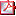 Imprimer Imprimer
Correction de l'exercice
II du DST de janvier 2006
Aventures ardéchoises
Exercice II 5,5 points
I.1. h = v(t-t0)
I.2. h = v(t-t0)
= 8 = 340(t - t0) soit (t - t0)
= 8/340 = 0,024 s La date d'arrivée est t = 13
h 31 min 24,024 s
I.3. L'onde sonore est longitudinale car le mouvement des éléments
du milieu (air) est parallèle à la direction de
propagation de l'onde.
I.4. l = cT =
c / f = 340 / 400 = 0,85 m
I.5. c = d / Dt =
1,51 / 7,2 = 0,21 m.s-1
I.6. L'onde à la surface de l'eau est une onde transversale
car le mouvement des éléments du milieu (eau) est
perpendiculaire à la direction de propagation de l'onde.
I.7. Cette onde déplacera GF verticalement, mais âs
horizontalement car la propagation de l'onde s'effectue sans
transport de matière.
II.1. Xm est l'amplitude, T0 est la période propre et f0 est la phase à l'origine.
II.2. 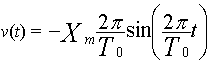
II.3. A la date t0 = 0, x(0) = Xm car cos 0 = 1
II.4. A la date t = 4,0 s, x(0) = Xm. En effet, avec T0
= 1/f = 1/2 = 0,5 s,
on a 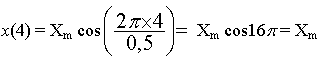
II.5. La hauteur des vagues est nulle aux dates 0,125 s ; 0,375
s ; 0,625 s et 0,875 s.
II.6. 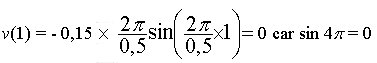
II.7. 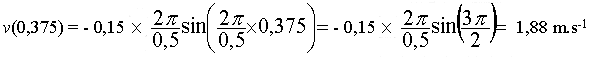
III.1. On mesure sur le dessin une distance de 1 cm entre deux
traits. Sachant que
l =cT = c/f =
340,0 / 340,0 = 1,0 m,
on en déduit que 1 cm représente 1 m.
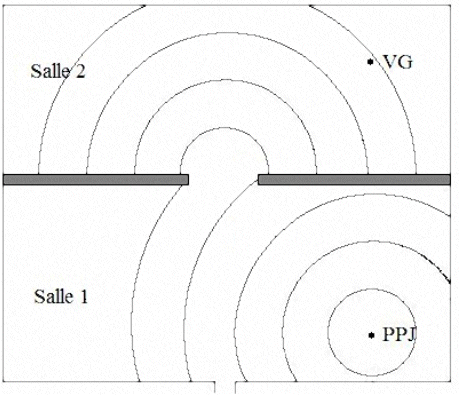
III.2.1. Représentation : les longueurs d'onde dans la
salle 1 et la salle 2 sont identiques.
III.2.2. La largeur de l'ouverture doit être de l'ordre
de 1 m, c'est à dire de l'ordre de grandeur de la longueur
d'onde.
III.2.3. Si l'ouverture avait été plus grande,
il n'y aurait pas eu de phénomène de diffraction
dont VG n'aurait pas bien entendu PPJ.
  Imprimer Imprimer
(Extrait de l'examen
blanc janvier 2005)
LES BORGS
"Resistance
is futile"
EPISODE I : A LA DECOUVERTE
DES BORGS
L'histoire commence en 2366
lorsque la Fédération des Planètes Unies
découvre qu'une espèce alien inconnue, appelée
les Borgs, veulent envahir la Terre.
Ce sont des êtres mi-homme mi-machine qui n'ont pour seul
but : assimiler
l'espèce humaine, c'est à dire de les transformer
comme eux.
 Un borg Un borg
Vous, élèves
de terminale S au Lycée Sainte Elisabeth en 2005,
vous allez être transporté temporellement en 2366
à bord de
l'USS Enterprise pour découvrir des Borgs et aider l'équipage
à résoudre le mystère des Borgs.
Le vaisseau galactique USS
Enterprise

Le capitaine Picard de l'USS
Enterprise a réussi lors d'une incursion dans l'espace
Borg,
a capturé un Borg encore fonctionnel. Il le soumet à
divers examens afin de mieux comprendre leur fonctionnement.

Jean-Luc Picard, commandant
du vaisseau galactique USS Enterprise.
L'un de ses examens consiste
à déterminer les caractéristiques visuelles
de l'œil d'un borg.
Il semble que les Borgs utilisent
une vision laser au dioxyde de carbone afin de déterminer
la dimension d'un objet.
Le laser à CO2 opère à des longueurs
d'onde comprises entre 9 mm et 11,5 mm.
I. Propriétés
du laser Borg.
1. Rappeler les limites des
longueurs d'onde du domaine du visible (en nm).
2. Les radiations du laser Borg font-elles partie du domaine
des UV ? des I.R. ? du visible ?
II. Observation
d'un phénomène lié au laser Borg.
On utilise le laser Borg produisant
une lumière de longueur d'onde l
placé devant un capteur positronique, constitué
d'une fente de largeur a et d'un écran.

Document 1
On observe la figure suivante,
constituée de tâches lumineuses, sur l'écran
positronique
placé à une distance D de la fente.
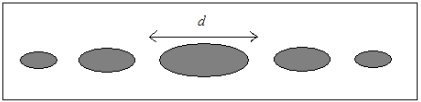
Document 2
1. Quel est le nom du phénomène
observé ?
2. Quelle condition doit satisfaire la taille de la fente pour
que l'on obtienne cette figure ?
3. La largeur de la taille centrale d sur l'écran varie
lorsque l'on fait varier la distance D
entre la fente et l'écran ; la longueur d'onde l de
la lumière, ou la largeur a de la fente.
Une série d'expérience
effectuées par le commandeur DATA, androïde unique
dont les capacités physiques et intellectuelles sont très
supérieures à celles des humains,
montrent que d est proportionnelle à la longueur d'onde
de la lumière.

Le commandeur DATA
k étant une constante
sans dimension, le commandeur DATA propose les formules (1),
(2), (3), (4) et (5) ci-dessous.
Laquelle ou lesquelles peut-il
éliminer ? Justifier vos réponses.
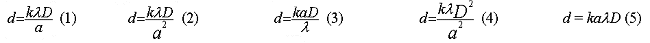
III. Influence
de la largeur de la fente du capteur positronique.
Tous les autres paramètres
restant inchangés pendant les mesures,
DATA fait varier la largeur a de la fente et mesure les valeurs
d correspondantes.
Les résultats sont consignés
dans le rapport scientifique n°1 .
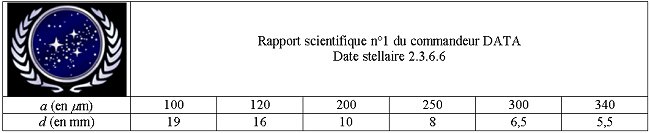
Grâce à ses résultats,
le commandeur DATA obtient les courbes suivantes :
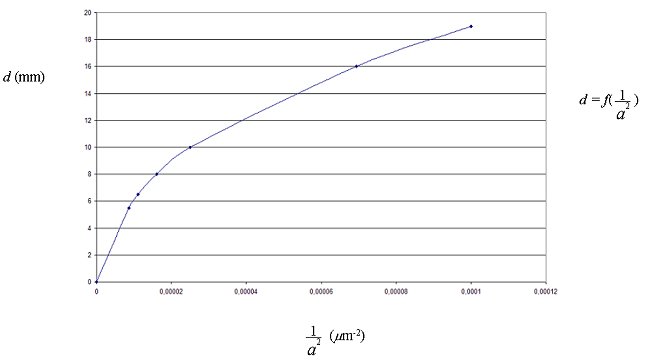
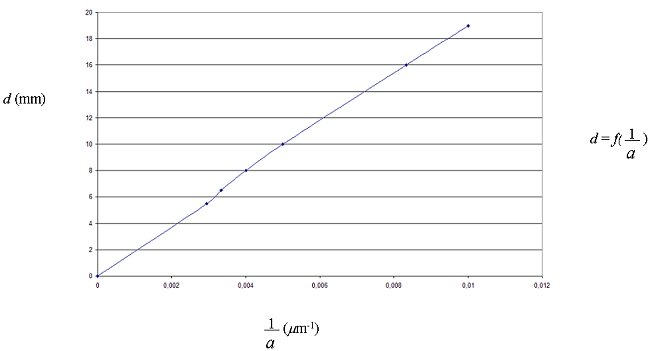
Préciser laquelle ou lesquelles des formules proposées
à la question II. 3 sont encore possibles.
Pourquoi ?
IV. Influence
de la distance D entre la fente et l'écran.
Le commandeur DATA fixe l et
a ; il déplace l'écran et il obtient les résultats
suivants :
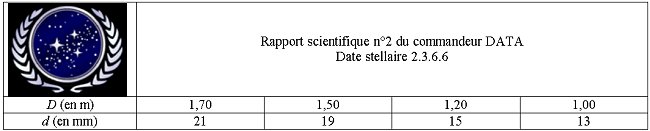
1. Quelle courbe est-il judicieux
de tracer pour vérifier la réponse à la
question III ?
Tracer la représentation graphique de cette courbe en
respectant l'échelle suivante :
Abscisse : 1 cm représente
0,1 m
Ordonnée : 1 cm représente 1 mm
2. Expliquer avec soin comment
calculer le coefficient directeur p de cette droite.
Déterminer la valeur de p.
3. En déduire la valeur
de k, sachant que c'est un entier, et que DATA a fait les
mesures pour l = 633 nm et a = 100 mm
V. Détermination
de la dimension d'un fil transwarp par la méthode Borg.
Un fil transwarp servant à
la conduction de l'antimatière dans le noyau du moteur
de l'enterprise,
placé à la position de la fente du dispositif précédent,
produit exactement la même figure sur l'écran.
DATA disposant d'un autre laser
de longueur d'onde l = 670 nm, décide de mettre en
œuvre
la même expérience utilisant la technologie Borg
pour mesurer le diamètre a du fil transwarp
qu'il a placé sur le support. Il obtient une tâche
centrale de largeur d = 20 mm lorsque
l'écran est à D = 1,50 m du fil transwarp.
Calculer le diamètre
du fil transwarp.
Vous venez de découvrir
ainsi l'incroyable acuité visuelle d'un Borg grâce
à sa vision laser.
  Imprimer Imprimer
Correction de l'examen
blanc sur les Borgs
Episode I.
I.1. Limites des longueurs
d'onde du domaine visible : 400 nm < lvisible
< 800 nm 0,25 point
I.2. Conversion 9 mm = 9 000 nm et 11,5 mm = 11
500 nm. Ces valeurs sont supérieures à 800 nm (Rouge),
les radiations du laser Borg
appartiennent au domaine des I.R. (Infrarouges). 0,5 point
II.1. Il s'agit du phénomène
de diffraction. 0,25 point
II.2. La taille de la fente doit être de l'ordre de grandeur
de la longueur d'onde. a < l. 0,5 point
II.3. Le texte indique que d est proportionnel à l, alors
on peut éliminer la formule (3) car dans ce cas d est
proportionnelle à 1/l.
De plus la (2) et la (5) ne sont pas valables car par analyse
dimensionnelle on constate que la relation n'est pas homogène
à la dimension d'une longueur. 0,5 point
III. On constate que d est
proportionnel à 1/a (droite passant par l'origine) alors
seule la formule (1) est encore possible. 0,5 point
IV.1. Il faut tracer la courbe
d = f(D). 0,25 point
IV.2. Pour déterminer
le coefficient p de la droite, on calcul le quotient de la différence
des ordonnés sur la différence des abscisses. 0,25
point
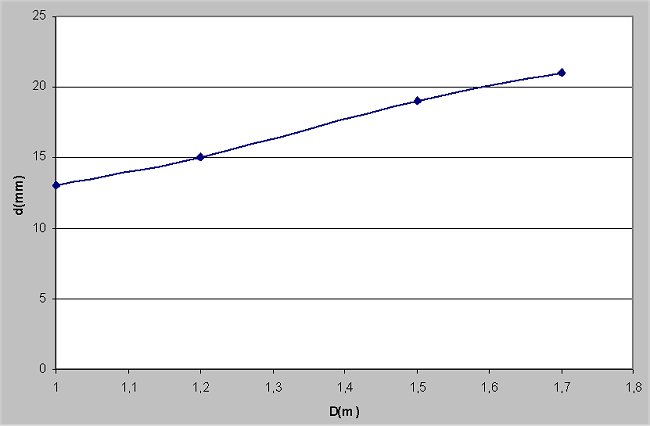
0,5 point
 0,5 point
0,5 point
IV.3.
 0,5 point 0,5 point
V. A partir de la relation
1,
on a :  0,5 point
0,5 point |