|
  Imprimer Imprimer
Les ondes mécaniques
progressives
I. Activités
expérimentales.
1. Onde
à une dimension : cas du ressort.
- Dispositif expérimental
: ressort à spires non jointives légèrement
tendu.
- Expérience : on pince 2 à 3 spires (compression)
et on lâche.
- Observation : propagation le long du ressort.

- Questions-Réponses
:
a. Quel est
le nom du phénomène observé ?
Il s'agit d'une onde mécanique
progressive.
Onde mécanique : qui
ne se propage pas dans le vide, qui a besoin d'un milieu matériel
pour se propager sans transport de matière.
La célérité
d'une onde mécanique dans les solides est supérieure
à celle dans les liquides, elle même supérieure
à celle dans les gaz.
b. Quelle est
la propriété du ressort qui permet la propagation
de cette onde progressive ?
Il s'agit de la propriété
d'être comprimé ou étiré.
c. Quel paramètre
physique permet de décrire la perturbation qui se propage
?
La distance qui sépare
deux spires consécutives.
d. Cette onde progressive est-elle
longitudinale ? Transversale ?
Longitudinale : si la direction du mouvement des
éléments du milieu de propagation est parallèle
à la direction de propagation.
Transversale : si la direction du mouvement des
éléments du milieu de propagation est perpendiculaire
à la direction de propagation.
Il s'agit d'une onde longitudinale.
2. Onde
à une dimension : cas de l'échelle de perroquet.
- Dispositif expérimental
: ruban élastique (acheté dans une mercerie) sur
lequel sont fixés des tiges (tiges en bois pour brochette)
perpendiculaires à l'axe du ruban. Des boules (boules
de couleurs pour les fêtes) sont fixées aux extrémités
des tiges.
- Expérience : on déplace la tige de l'une extrémités
et on laisse revenir dans sa position d'équilibre.
- Observation : propagation de la perturbation orthogonalement
à la direction de propagation.

- Questions-Réponses :
a. Quel paramètre permet
de décrire la perturbation qui de propage ?
L'angle de la tige par rapport
au plan initial ou la distance qui sépare la tige du plan
intial.
b. Cette onde progressive est-elle
longitudinale ou transversale ?
Il s'agit d'une onde transversale
car la direction du mouvement des éléments du milieu
de propagation est perpendiculaire à la direction de propagation.
c. Qu'appelle-t-on une onde
à une seule dimension ?
Une onde est à une dimension
quand la position d'un point du milieu est parfaitement déterminé
par son abscisse.
d. De quoi dépend la célérité de
l'onde ?
La célérité
de l'onde dépend de :
- l'inertie du système
= masse des boules (masselottes)
Si la masse augmente alors la célérité diminue
- de la tension du ruban.
Si la tension du ruban augmente alors la célérité
augmente.
3. Onde
à deux dimensions : onde à la surface de l'eau.
- Dispositif expérimental
: video.
- Expérience : on créé une onde en un point
de la surface de l'eau en laissant tomber une pierre.
- Observation : propagation de l'onde dans toutes les directions
de la surface.

- Questions-Réponses :
a- Il y a-t-il déplacement
de l'eau du point d'impact vers l'extérieure ? Comment
le montrer expérimentalement ?
Non, il n'a pas de déplacement
d'eau vers l'extérieur ?
Il y a transfert d'énergie mais pas de transport de matière.
Expérience possible
: mettre un objet flottant et observer s'il se déplace.
On observe un déplacement de bas en haut, mais pas de
déplacement vers l'extérieur.
b- Cette onde est-elle transversale
? longitudinale ?
Il s'agit d'une onde transversale
(voir justification plus haut)
c- Combien de coordonnées
sont nécessaires pour déterminer la position d'un
point de l'onde ?
Deux coordonnées x et
y. Il s'agit d'une onde à deux dimensions.
4. Onde
à trois dimensions : cas du son.
Les vibrations sonores correspondent
à de petits déplacements longitudinaux (variation
de pression) autour d'une valeur moyenne dans la direction de
la propagation.
Il s'agit d'une onde longitudinale
car la propagation de la compression-dilatation s'effectue parallèlement
à la direction de propagation.
Une onde sonore est à
trois dimensions car la position d'un point du milieu est parfaitement
déterminé par trois coordonnées.

- Questions-Réponses
:
a- selon vous, un son fort
se déplace-t-il plus vite, moins vite ou aussi vite qu'un
son faible ?
La vitesse de dépend
pratiquement pas du type de son, elle dépend du milieu.
b- selon vous, un son grave
se déplace-t-il plus vite, moins vite ou aussi vite qu'un
son aiguë ?
Dans un milieu non dispersif
(air pur), la vitesse du son ne dépend pas de la fréquence
du son.
c- Selon vous , un son va-t-il
plus vite, moins vite, aussi vite dans l'air, dans l'eau ou dans
un solide ?
La vitesse du son vsolide
> veau > vair La
vitesse dépend de la compressibilité du milieu.
d- Si nous plaçons une
bougie allumée devant un haut parleur qui émet
un son fort, continu et aiguë, la flamme bougera-t-elle
? Si le haut parleur émet un son grave, qu'en est-il ?

Expérience pour illustrer cette question.
Un haut parleur est alimenté par un GBF délivrant
un son de fréquence réglable.
Avec un son aigu (f = 10 000 Hz) la flamme n'est pas affecté
par l'émission sonore.
Par contre, la flamme vacille un peu quand le son grave (f
= 50 Hz)
e- Comment expliquez-vous que
la voix mélodieuse de votre professeur soit moins audible
au fond de la classe que devant ?
L'affaiblissement est dû
au fait que la puissance sonore par une unité de surface
est plus faible quand on s'éloigne de l'émetteur.
II. Bilan des activités
expérimentales.
1. Définition.
On appelle onde mécanique
le phénomène de propagation d'une perturbation
dans un milieu sans transport de matière.
2. Les ondes
transversales :
Une onde est transversale si
la direction du mouvement des éléments du milieu
de propagation est perpendiculaire à la direction de propagation.
Exemples :
o Onde le long d'une corde.
o Onde à la surface de l'eau.
o Onde de torsion sur l'échelle de perroquet.
o Certaines ondes sismiques.
3. Les ondes
longitudinales :
Une onde est longitudinale
si la direction du mouvement des éléments du milieu
de propagation est parallèle à la direction de
propagation.
Exemples :
o Onde le long dans un ressort.
o Onde de pression dans un solide, liquide ou gaz (onde sonore)
o Certaines ondes sismiques.
III. Propriétés
générales des ondes.
1. Une onde se propage, à
partir de la source, dans toutes les directions qui lui sont
offertes (milieu à 1, 2 ou 3 dimensions)
2. La perturbation se propage de proche en proche. Il y a transfert
d'énergie, sans transport de matière.
- Dans la plupart des cas,
on observe une diminution de l'amplitude de l'onde due à
un transfert d'énergie au milieu de propagation (travail
des forces de frottement, viscosité, friction).
- Elongation : position d'un point du milieu par rapport à
son position d'équilibre.
- Amplitude : valeur maximale de l'élongation.
3. La vitesse de propagation
d'une onde est une propriété du milieu.
- La célérité
: 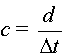 c (m.s-1) d (m) Dt (s)
c (m.s-1) d (m) Dt (s)
- La célérité est caractéristique
du milieu.
- La célérité est indépendante de
la forme et de l'amplitude du signal (si l'amplitude reste faible)
- La célérité dépend du type d'onde
qui se propage :
Une onde transversale à
la surface de l'eau a une célérité beaucoup
plus faible. qu'une onde de pression longitudinale qui se propage
dans le liquide.
Voir TP n°2.
- La célérité
d'une onde de torsion diminue quand on augmente l'inertie du
milieu (augmente de la masse des masselottes) et quand on augmente
la tension (tension du ruban élastique)
- La célérité dépend de la compressibilité
du fluide :
La célérité
d'une onde progressive est plus grande dans l'eau que dans l'air.
4. Deux ondes peuvent se croiser
sans se perturber.
Voir page 26 du livre, figure
20.
Deux cailloux lancés
dans l'eau génèrent des ondes circulaires qui se
croisent sans se perturber.
IV. Onde progressive à
une dimension.
1. Définition
(voir livre page 27)
: une onde mécanique progressive à une dimension
est une onde qui ne se propage que dans une seule direction.
2. Notion de retard
(voir livre page 27, figure 21).
La perturbation au point M'
à l'instant t' est celle qui existait auparavant en un
point M à l'instant t = t' - t
t est le retard
avec 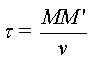 t (s) MM' (m) v : célérité (m.s-1)
t (s) MM' (m) v : célérité (m.s-1)
La perturbation en un point
à l'instant t est celle qu'avait la source à
la date t' = t - t
Cette relation est valable
pour les milieux non dispersifs.
Un milieu est dispersif si
la célérité dépend de la fréquence
de l'onde.
  Imprimer Imprimer
Les ondes
progressives mécaniques périodiques
I. Exemples dans la vie
courante d'ondes mécaniques progressives périodiques.

Questions-réponses :
Question : Proposer des exemples
et trouvons le point commun entre-eux :
Réponses :
- Les vagues de houle (page 40 figure 8)
o propagation à la surface de l'eau.
o Période T = 10 s
- Les marées
o Origine : action gravitationnelle de la Lune et du Soleil
o Période T = 12 h 25 minutes (entre deux pleines
mers)
- Une note de musique
o Le " La " de fréquence f = 440 Hz,
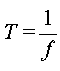 = 0,0023 s
= 0,0023 s
Le point commun entre ces exemples
est le fait qu'ils se répètent identiquement à
eux mêmes à intervalles de temps égaux.
II. Définition d'une
onde progressive mécanique périodique et mise en
évidence expérimentale de sa double périodicité.
1. Définition.
Une onde progressive mécanique
périodique est le phénomène qui accompagne
la propagation d'une perturbation qui se répète
identique à elle même à intervalles de temps
égaux.
2. Mise
en évidence expérimentale de la double périodicité
du phénomène.
2.1. Périodicité
temporelle.
2.1.1. Mise en évidence
expérimentale.
Un GBF alimente un haut parleur
par une tension périodique de fréquence f
= 4 000 Hz soit T = 2,5 x 10-4 s.
Le haut parleur alimenté par le GBF émet une onde
sonore progressive périodique.
Un microphone capte le son émis.
On lit sur un oscilloscope la fréquence du son reçu.
La fréquence est égale à fmicro
= 4 000 Hz.
2.1.2. Définition de
la période temporelle T.
La période temporelle
est la plus courte durée au bout de laquelle le phénomène
se reproduit identique à lui-même.
C'est la durée au de laquelle un point du milieu se retrouve
dans le même état vibratoire.
Elle est notée T et s'exprime en seconde.
2.2. Périodicité
spatiale.
2.2.1. Mise en évidence
expérimentale.
Un GBF alimente un haut parleur
par une tension périodique de fréquence f
= 4 000 Hz soit T = 2,5 x 10-4 s.
Deux microphones sont placés
devant le haut parleur.
Les deux microphones sont reliés à un oscilloscope
bicourbe.
Le premier est à 12,0 cm du haut parleur.
On éloigne le microphone 2 du microphone 1 qui passe de
la position A à une position B, telle les deux signaux
sinusoïdaux se retrouve en phase.
On mesure la distance de séparation
entre les deux microphones d = 9,0 cm.
Si on éloigne à
nouveau le microphone 2 de 9,0 cm les signaux sont à nouveau
en phase.
2.2.2. Définition.
On appelle période spatiale
ou longueur d'onde, notée l, la plus petite distance séparant
deux points pour lesquels les perturbations sont en phase.
3. Relation
l = v.T. Application à la détermination de la célérité
d'une onde sonore.
3.1. Mise en évidence
expérimentale.
Dans l'expérience précédente
pour une fréquence f1 = 4 000 Hz, on avait :
- f1 = 4 000
Hz
- T1 = 2,5
10-4 s.
- l1
= 9,0 x 10-2 m (mesure)
Lors d'une nouvelle avec une
fréquence f2 = 6 000 Hz, on a :
- f2 = 6 000
Hz
- T2 = 1,67
10-4 s
- l2 = 6,0 10-2 m (mesure)
3.2. Exploitation et interprétation
des résultats.
On constate que 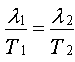 = 340 unité (m.s-1) Cette constante à
la grandeur d'une célérité.
= 340 unité (m.s-1) Cette constante à
la grandeur d'une célérité.
La relation entre l et T est alors l
= vT ou encore 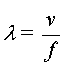
l (m) , T (s) et
f (Hz)
On peut retrouver l'unité
de la célérité à partir des unités
de la période et de la longueur d'onde en posant une équation
aux dimensions.
On note [T] la dimension de
la période et [L] la dimension de la longueur d'onde.
L'équation aux dimensions s'écrit [L] = [v].[T]
Alors la dimension de v est [v] = [L].[T]-1 v
a bien la dimension d'une célérité (vitesse).
La longueur d'onde l
est égale à la distance parcourue par l'onde pendant
une période T.
III. La diffraction, mise
en évidence expérimentale.
1. Essayons
de prévoir le phénomène de diffraction.
Le schéma ci-dessous
représente une cuve à onde contenant de l'eau dans
laquelle la pointe ou la lame d'un vibreur est plongé.
On place une paroi muni d'une fente dans l'eau.

Questions-réponses :
Selon, quelle sera l'allure
de la surface de l'eau dans la partie gauche de la cuve ?
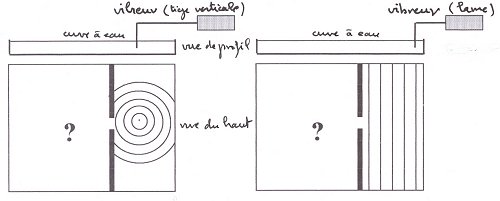
Confrontons vos prévisions
avec la simulation suivante d'un phénomène de diffraction.
Logiciel de simulation : Wavelab
de 7P soft
Télécharger ce
logiciel en le trouvant par recherche sur Google (par ex.)en
utilisant les mots clés " wavelab 7P Soft "
2. Observation
du phénomène de diffraction.
Image de diffraction : page
43 figure 16a.
Questions-réponses :

- la longueur d'onde l
a-t-elle été modifiée après passage
par la fente ?
Non, la longueur d'onde est
inchangée
- La fréquence (rythme
du vibreur) a-t-elle été modifiée ?
Non, la fréquence est
inchangée car on a pas modifié le rythme du vibreur.
La fente se comporte comme
une source ponctuelle donnant naissance à des ondes circulaires.
Tous les points de l'espace situé derrière la fente
sont atteint par l'onde.
3. Quelle
est l'influence de la taille de l'ouverture ou de l'obstacle
sur le phénomène de diffraction ?
Logiciel de simulation : Wavelab
de 7P soft
Expérience 1 : Largeur
de la fente a inférieure ou égale à
la longueur d'onde l.
Image de diffraction : page
43 figure 16a. 
Expérience 2 : Largeur
de la fente a supérieure à la longueur d'onde l.
Image de diffraction : page
43 figure 16 b, 16c 
Interprétation :
Expérience 1 : a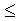 l l
- Tous les points de l'espace
situé derrière la fente sont atteint par l'onde.
- On obtient une onde diffractée sphérique centrée
sur la fente.
Expérience 2 : a
> l
- Dans certaines directions
l'onde diffractée est nulle si a un peu plus grand
que l.
- Pas de phénomène de diffraction (hormis au voisinage
immédiat des bords de la fente) si a beaucoup plus
grand que l.
4. Conclusion
: définition du phénomène de diffraction.
On appelle diffraction l'ensemble
des phénomènes qui accompagnent la propagation
d'une onde après interaction avec une ouverture ou un
obstacle dont la dimension est de l'ordre de la longueur d'onde
l.
Le phénomène
de diffraction est d'autant plus marqué que l'ouverture
ou l'obstacle est plus petite.
IV. Le phénomène
de dispersion.
On a montré que, dans
l'air sec, toutes les ondes sonores ont la même célérité
quelque soit leur fréquence.

Questions-réponses :
1. Comment
expliquer alors, le grondement sourd et tardif du bruit du tonnerre
?
Sachant que :
- L'air est chargé en
vapeur d'eau.
- L'amplitude du bruit du tonnerre est très grande.
- Les sons aiguës nous parviennent avant les sons graves.
Bruit
de tonnerre

Réponse :
Pour ce type d'onde, on dit
que l'air chargé en vapeur d'eau est un milieu dispersif.
La célérité des ondes de haute fréquence
est plus élevée que celles de basse fréquence
?
Autre exemple avec l'eau :
- La célérité
de la houle en haute mer varie avec la période.
- La célérité d'une onde dans une cuve à
onde contenant une couche d'onde peu profonde varie avec la période.
2. Conclusion
: Définition d'un milieu dispersif.
Un milieu de propagation est
dispersif quand la célérité de l'onde périodique
dépend de sa fréquence.
V. Ondes progressives sinusoïdales.
1. Définition
d'une grandeur sinusoïdale.
Une grandeur physique est sinusoïdale
ou harmonique si elle peut être décrite par une
fonction sinusoïdale de la forme :
y = A sin q ou y = A cos q
y : élongation du signal
A : amplitude de la grandeur y
q : angle appelé phase de l'onde (c'est
une variable)
Si y est une fonction
du temps alors la phase q prend la valeur 2p pour t
= T. (période)
q peut s'écrire 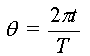
On appelle phase à l'origine, notée j,
la valeur de la phase à l'instant t = 0.
On peut écrire 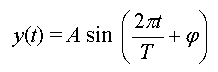
On écrit parfois y(t) = A sin (wt + j) avec 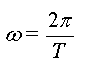 w est la pulsation (rad.s-1)
w est la pulsation (rad.s-1)
2. Une sinusoïde
est définie par sa période, son amplitude et sa
phase à l'origine.

Questions-réponses :
Comparer les caractéristiques
des sinusoïdes représentées ci-dessous.
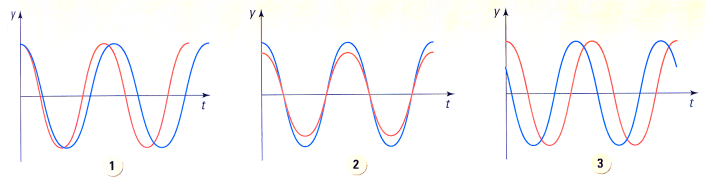
Ont-elles la même amplitude ? la même période
? la même phase à l'origine ?
On note :
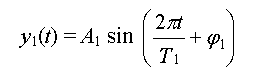 courbe rouge (courbe claire en tirage noir et blanc)
courbe rouge (courbe claire en tirage noir et blanc)
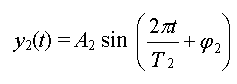 courbe bleu (courbe foncée en tirage noir et blanc)
courbe bleu (courbe foncée en tirage noir et blanc)
Réponses :
Cas n° 1 : les deux courbes
ont
- la même amplitude A1
= A2
- la même phase à l'origine j1 =
j2
- des périodes différentes T1 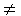 T2 T2
Cas n° 2 : les deux courbes
ont
- des amplitudes différentes
A1 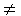 A2 A2
- la même phase à l'origine j1 =
j2
- la même période T1 = T2
Cas n° 3 : les deux courbes
ont
- des amplitudes différentes
A1 = A2
- des phases à l'origine différentes j1
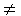 j2 j2
- la même période T1 = T2
3. En un
point donnée, comment évolue l'élongation
y au cours du temps ?
Au niveau de la source : yS(t)
= A sin
On choisit comme conditions à l'origine j
= 0 à t = 0
Alors 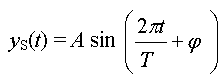
Expression de l'élongation
du point M situé à une distance x de la
source :
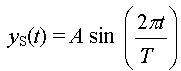
Le sens de propagation est celui de l'axe Ox
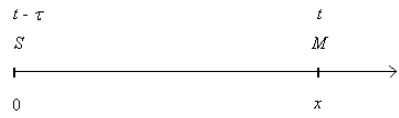
L'élongation yM
du point M d'abscisse x à la date t est
égale à l'élongation yS
du point S à la date t - t.
C'est à dire que le
point M a le même mouvement que la source avec un retard
t.
On peut alors écrire
:
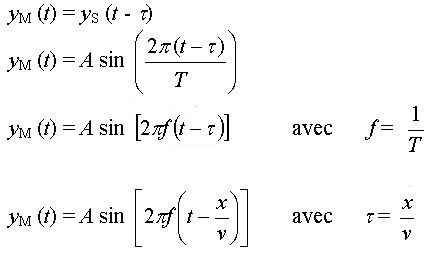
 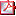 Imprimer Imprimer
La lumière,
modèle ondulatoire
I. TP-Cours : Observation
expérimentale de la diffraction en lumière monochromatique.

1. Expérience.
Position du problème
:
· Réaliser un
montage permettant de mettre en évidence le phénomène
de diffraction et montrer ainsi que la lumière peut être
décrite comme une onde.
· Vérifier la pertinence de la relation 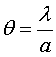
- Réaliser le montage
suivant :
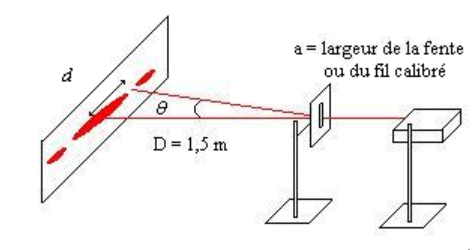
d : distance entre le centre de la frange lumineuse centrale
et la première extinction.
D : distance entre l'écran (mur) et la fente. D
= 1,5 m.
a : largeur de la fente ou du fil calibré.
l : longueur d'onde de la lumière du laser. l
= 650 nm.
- Placer une feuille de papier
millimétré sur le mur et relever la taille de la
frange lumineuse centrale en mesurant la distance 2d entre les
deux premières extinctions.
- Réaliser cette mesure pour différentes largeurs
de fente ou de fil calibré.
- Etablir la relation entre d, D et q.
- Compléter le tableau suivant :


Questions et interprétation
:
· Dans quelle direction
les taches de diffraction s'étalent-t-elles par rapport
à la direction de la fente ?
· la relation 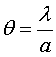 est-elle vérifiée ? est-elle vérifiée ?
Pour consulter les résultats
du TP, cliquer TP n°3.
2. Exploitation
du TP.
- La lumière étant
diffractée, peut être considéré comme
une onde.
- Plus la dimension a de l'obstacle (fil calibré) ou de
l'ouverture (fente) est petite, plus la tache de diffraction
est grande.
 |
 |
|
Fil de 120 mm de diamètre |
Fil de 40 mm de diamètre |
- La tache de diffraction est
perpendiculaire à l'axe du fil calibré ou de la
fente.
- On a la relation 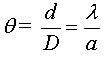
l étant la longueur d'onde de la lumière
monochromatique. Unité : (m)
a étant la largeur du fil calibré ou de
la fente. Unité : (m)
II. Propagation de la lumière
dans le vide.
1. Célérité
de la lumière dans le vide.
La célérité
est une constante universelle. c = 299 792 458 m.s-1
2. Les couleurs
de la lumière.
- Une onde lumineuse de fréquence
n transporte de l'énergie électromagnétique.
- Les ondes lumineuses sont périodiques.
- La longueur d'onde l est relié à la célérité
c par la relation 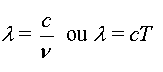
n étant la fréquence exprimé
en Hertz (Hz).
T la période exprimé en seconde (s)
l la longueur d'onde exprimé en mètre
(m)
- Une lumière monochromatique
est une onde lumineuse unique de fréquence donnée.

Question-Réponse :
Citer un exemple de lumière
monochromatique.
Exemple : La lumière
d'un LASER He-Ne est quasiment monochromatique
n = 4,741 x 1014 Hz ou l
= 632,8 nm
- Une lumière polychromatique
est constituée de plusieurs ondes lumineuses de fréquences
différentes.

Question-Réponse :
Citer un exemple de lumière
polychromatique.
Exemple : La lumière
du Soleil, d'une lampe…
3. le spectre
visible.
- L'œil est sensible à
l'énergie transportée par l'onde lumineuse.
- Cette sensibilité dépend de la fréquence.
Limites des longueurs d'onde
dans le vide du spectre visible :
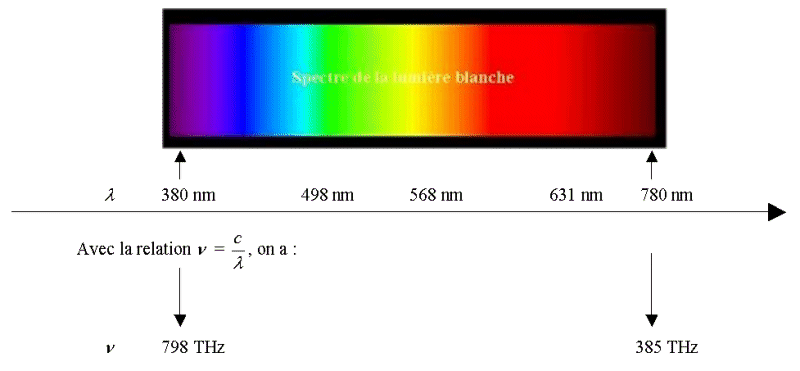
1 Térahertz
= 1,0 x 1012 Hz.
1 nm = 1,0 x 10-9 m
4. Au-delà
du visible.

Question-Réponse.
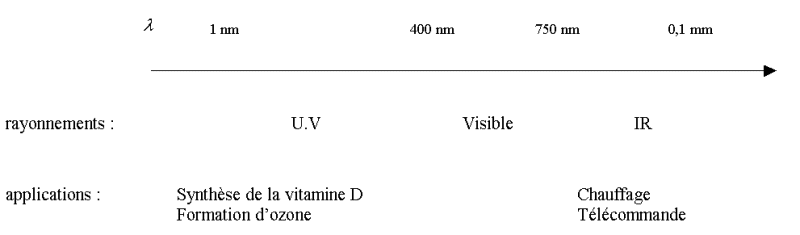
A partir du document page 63,
figure 18, placer dans leur domaine de longueur d'onde l respectif,
les différentes ondes électromagnétiques
suivantes :
Infra-rouge (I.R) , Ultra-violet (U.V) , Visible.
Donner des exemples d'applications
de des rayonnements U.V et IR.
Réponse :
III. La lumière se
propage dans les milieux transparents.
1. Indice
n d'un milieu.
- L'onde lumineuse se propage
dans le vide, mais également dans un milieu transparent
et isotrope (conservation des propriétés du milieu
dans toutes les directions de l'espace).
- Dans un milieu autre que le vide :
la célérité
v de l'onde lumineuse dans un milieu transparent est plus
faible que celle dans le vide. v < c.
- On caractérise un
milieu par son indice n, appelé également indice
de réfraction.
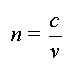 c (m.s-1) v (m.s-1) n
(sans dimension) n > 1
c (m.s-1) v (m.s-1) n
(sans dimension) n > 1
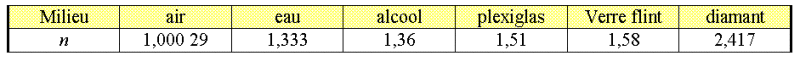
2. La fréquence
d'une radiation chromatique ne change pas lorsqu'elle passe d'un
milieu transparent à un autre.

Question-réponse :
La longueur d'onde d'une radiation
chromatique dans un milieu d'indice n est-elle différente
que dans le vide ?
Réponse :
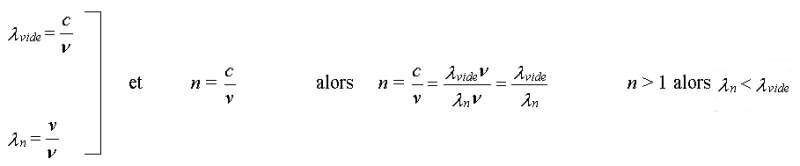
IV. Les milieux transparents sont plus ou moins dispersifs.
1. exemple
de l'eau.

Question-réponse :
Interpréter les résultats
consignés dans le tableau ci-dessous.
L'eau est-il un milieu dispersif ?

- La célérité
de la lumière dans l'eau dépend de la longueur
d'onde (ou de la fréquence) du rayonnement lumineux.
- L'indice du milieu dépend également de la longueur
d'onde (ou de la fréquence) du rayonnement lumineux.
- L'eau est donc un milieu
dispersif.
2. un prisme
disperse la lumière.

Expérience :
On éclaire avec une
source lumineuse un prisme comme indiqué sur la photo
suiavnte :

Source : futura sciences
Ou on peut visionner une expérience
réalisée à l'IUFM de Nice
http://www.iufm.unice.fr/application/spip/article.php3?id_article=315
Page 65, figures 21 et 22.
L'indice du milieu dépendant
de la fréquence des différentes radiations lumineuses,
celles-ci sont déviées différemment (lois
de Descartes sur la réfraction).
La lumière blanche est décomposée par le
prisme.
La radiation violette est plus déviée que la radiation
rouge car quand l diminue, n croît (ou
quand n augmente, n diminue) |