|
  Imprimer Imprimer
Noyaux, masse, énergie
I. Equivalence masse-énergie.
1. Défaut
de masse.
Les physiciens ont constatée
que la masse d'un noyau était moins élevée
que la masse de ces constituants, ce qui contredit les lois de
conservation que Lavoisier avait proposé.
Pour le noyau d'hélium
:

Le défaut de masse est
égal à Dm = 0,0305 x 10-27kg
 > 0
> 0
Une question se pose : mais
où donc est passée la masse manquante ?
2. Energie
de liaison.
L'énergie de liaison
El est l'énergie qu'il faut fournir à
un noyau au repos pour le dissocier en ces différents
constituants (nucléons).
Ou encore, l'énergie
de liaison correspond à l'énergie que les protons
et les neutrons doit céder pour former un noyau.
Il y aurait-il un rapport entre
défaut de masse et énergie de liaison ? Posons
la question à Monsieur Albert Einstein.
3. Equivalence
masse-énergie.
Albert Einstein postula en
1905 le principe d'équivalence masse-énergie.
" Tout corps au repos
possède du seul fait de sa masse, une énergie E
= mc2k appelée énergie de masse ".
L'énergie E s'exprime
en Joule (J)
La masse m s'exprime en kilogramme (kg)
La célérité de la lumière dans le
vide c = 2,9979 x 108 m.s-1 c 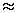 3,0 x 108m.s-1
3,0 x 108m.s-1
Ainsi le défaut de masse
obtenu dans le cas du noyau d'hélium correspond à
l'énergie de liaison

L'énergie de liaison
a pour expression générale :

4. Les unités
utilisées en physique nucléaire.
4.1. L'énergie (J).
l'électron-volt (eV)
le méga électron volt (MeV)
1 eV = 1,6 x 10-19
J 1 MeV = 1,0 x 106 eV = 1,6 x 10-13J

Question discussion réponse:
Déterminer en MeV, l'énergie
correspondant à la masse d'un électron me
= 9,1 x 10-31 kg
Réponse :

4.2. La masse (kg).
- L'unité de masse atomique
(u)

 représente
la masse du noyau représente
la masse du noyau
 représente
la masse d'un nucléon représente
la masse d'un nucléon

Pour ceux qui sont observateurs,
vous constaterez que
1 u = 1,66054 x 10-27kg
est inférieure à la masse d'un proton ou d'un neutron.

Question discussion réponse :
Comment expliquez-vous que
1 u soit inférieure à la masse d'un proton ou d'un
neutron ?
Réponse :
Le calcul de l'unité
de masse atomique a été effectué à
partir de la masse d'un noyau.
Comme on l'a vu précédemment,
un nucléon au sein d'un noyau pèse moins lourd
qu'un nucléon isolé !

- Le MeV/c2
Le Mev/c2 est une unité
de masse définie à partir de la relation d'équivalence
L'énergie correspondant
à une masse de 1 u est égale à 
On a  alors 1 u = 931,5 MeV/c2
alors 1 u = 931,5 MeV/c2
L'intérêt de cette
unité est de faire directement la correspondance entre
une énergie et une masse.
5. Mise
en évidence de l'intérêt énergétique
des réactions de fission et de fusion par l'étude
de la courbe d'Aston 
5.1. L'énergie de liaison
par nucléon 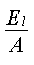
L'énergie de liaison
par nucléon 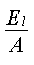 permet de comparer la stabilité des différents
noyaux afin de prévoir la nature d'éventuelles
réactions nucléaires.
permet de comparer la stabilité des différents
noyaux afin de prévoir la nature d'éventuelles
réactions nucléaires.
L'énergie de liaison
par nucléon 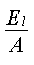 a pour unité MeV/nucléon.
a pour unité MeV/nucléon.
Plus l'énergie de liaison
par nucléon est élevée plus le noyau est
stable.
Exemples :


Question discussion réponse
:
Quel est le noyau le moins
stable parmi les 3 cités dans le tableau ?
Réponse :
Le deutérium
5.2. La courbe d'Aston.
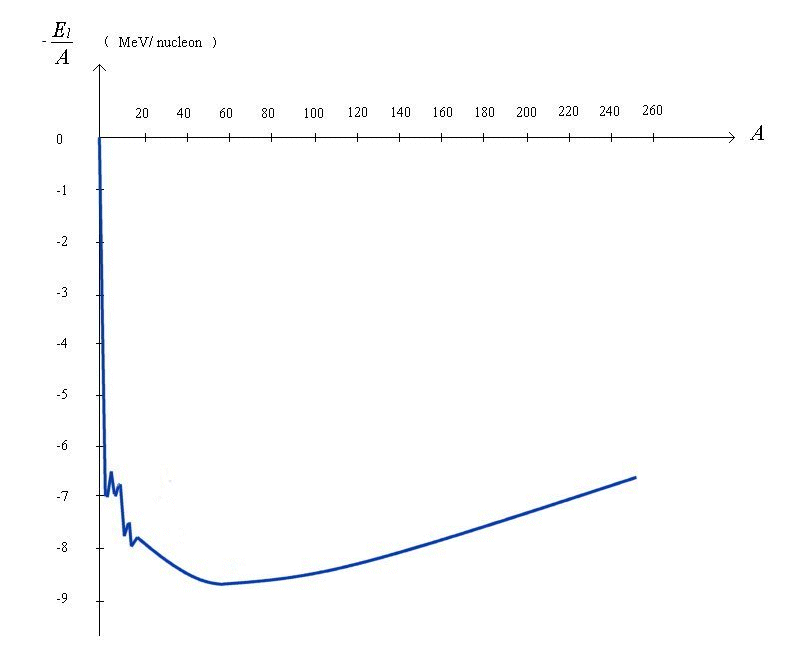
Analyse de la courbe d'Aston

Question discussion réponse
Sur la photocopie de la courbe
d'Aston dont vous disposez, indiquez :
- dans quelle zone se situent
les noyaux les plus liés (les plus stables)
- parmi les noyaux suivants, quel est selon le plus stable  , , ou
ou  ? ?
- dans quelles zones se situent les noyaux les moins liés
(les moins stables) ?
- dans quelle zone peut-on prévoir des réactions
de fusion nucléaire ?
- dans quelle zone peut-on prévoir des réactions
de fission nucléaire ?
Réponses :
- Les noyaux les plus liés
sont ceux dont l'énergie de liaison par nucléon
est la plus élevée (en valeur absolue). Ils sont
situés dans la zone centrale (voir schéma ci-dessous)
- Le noyau de fer 56 est le plus stables car son énergie
de liaison par nucléon est la plus élevée.
- Les noyaux les moins liés sont situés aux extrémités
de la courbe d'Aston.
- Les réactions de fusion nucléaire affecteront
les noyaux les plus légers.
- Les réaction de fission nucléaire affecteront
les noyaux les plus lourds.

  Imprimer Imprimer
II. Fission et fusion.
1. La physique
nucléaire dans l'histoire.

Question discussion réponse
:
Associer la date correspondant
à l'événement relatif au nucléaire.
1898 La fission nucléaire
est découverte par des physiciens allemands
1939 Première explosion d'une bombe nucléaire A
1939 Explosion de la première bombe H
1942 Première bombe atomique française
1945 Le réacteur à fusion nucléaire expérimental
ITER à Cadarache.
1952 L'accident de Tchernobyl
1960 Pierre et Marie Curie découvrent le radium
1986 Le Projet Manhattan est lancé par la Maison Blanche
1997 Frédéric Joliot-Curie découvre la réaction
en chaîne
2005 Signature du Traité d'interdiction complète
des essais nucléaires
Réponse :
1898 Pierre et Marie Curie
découvrent le radium
1939 Frédéric Joliot-Curie découvre la réaction
en chaîne
1939 La fission nucléaire induite est découverte
par des physiciens allemands
1942 Le Projet Manhattan est lancé par la Maison Blanche
1945 Première explosion d'une bombe nucléaire A
1952 Explosion de la première bombe H
1960 Première bombe atomique française
1986 L'accident de Tchernobyl
1997 Signature du Traité d'interdiction complète
des essais nucléaires
2005 Le réacteur à fusion nucléaire expérimental
ITER à Cadarache.
Source : http://www.linternaute.com/histoire/nucleaire/67/a/1/1/3/
2. La fission
nucléaire.
2.1. Définition.
Lors d'une fission nucléaire,
un noyau lourd A > 200 se scinde en deux noyaux plus légers
sous l'impact d'un neutron.
Le noyau est dit " fissile
".
2.2. Exemple de fission nucléaire.
Le noyau d'uranium 235 a plusieurs
possibilités de fission. En voici une :
 Sr : Strontium Xe : Xénon
Sr : Strontium Xe : Xénon
Les lois de conservations sont
vérifiées.
- conservation du nombre de
charge 92 = 38 + 54
- conservation du nombre de nucléon 235 + 1 = 94 + 140
+ 2 x 1
Remarque : on ne simplifie
pas les neutrons dans l'équation car ils ne sont pas équivalents
!

Question discussion réponse :
En appliquant les lois de conservation,
compléter l'équation de la réaction de fission
suivante :

Réponse :
 Br : brome La : Lanthane
Br : brome La : Lanthane
- conservation du nombre de
charge 92 = 35 + 57
- conservation du nombre de nucléon 235 + 1 = 85 + 148
+ 3 x 1
2.3. Réaction en chaîne.
Page 107 figure 9
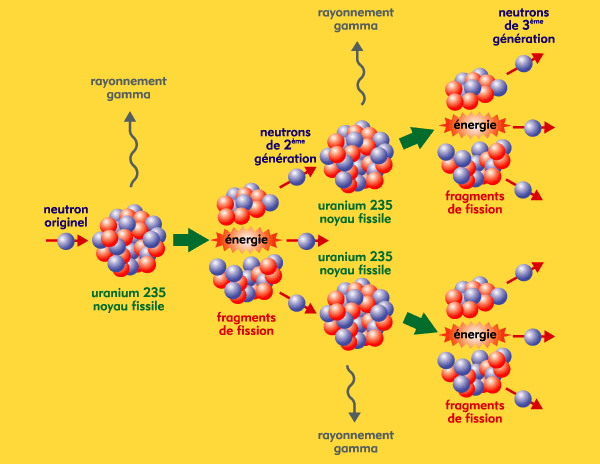 Source : CEA
Source : CEA
Conditions pour obtenir l'amorçage
des réactions de fission :
- il faut que le noyau lourd
(uranium 235) soit percuté par un neutron.
- Il faut que dans un certain volume la masse des noyaux fissiles
soit suffisante (masse critique).
2.4. Fission contrôlée.
|
En 1963, EDF produit
pour la première fois de l'électricité nucléaire
dans la centrale EDF1 sur le site de Chinon.
En 1974 la France choisit le
nucléaire
Le Premier ministre Pierre
Messmer annonce le lancement d'un vaste programme nucléaire
qui prévoit de limiter la consommation de pétrole
au profit de l'atome. Entre 1974 et 1975, 13 nouvelles centrales
nucléaires seront lancées par EDF. |
La production d'énergie
dans les centrales nucléaires à partir d'1 gramme
d'uranium 235 est équivalente à celle libérée
par 1 tonne de pétrole.
Le contrôle de la fission
s'effectue grâce à des barres de graphite qui arrêtent
les neutrons.
3. La
fusion nucléaire.
3.1. Définition.
Lors d'une réaction
de fusion nucléaire, deux noyaux légers s'agglomèrent
en un noyau plus lourd et plus stable.
3.2. Exemple de réaction
de fusion nucléaire.
 : deutérium : protium
: deutérium : protium
Les lois de conservation sont
vérifiées :
- conservation du nombre de
charge 1 + 1 = 2
- conservation du nombre de nucléon 2 + 1 = 3

Question discussion réponse
:
En appliquant les lois de conservation,
compléter l'équation de la réaction de fusion
suivante :

Réponse :

- conservation du nombre de
charge 2 + 2 = 2 + 2 x 1
- conservation du nombre de nucléon 3 + 3 = 4 + 2 x 1
3.3. La réaction en
chaîne dans les étoiles.
Condition pour obtenir l'amorçage
des réactions de fusion :
Pour amorcer une réaction
de fusion nucléaire , il faut élever la température
à plus
d'un million de kelvin pour vaincre la répulsion coulombienne
qui s'exercent entre les protons.
Ces conditions extrêmes
existent au sein des étoiles où la température
est de l'ordre de
plusieurs dizaines de millions de degrés.
La nébuleuse
d'Orion (photo : Philippe Morin)
Une réaction en chaîne
débutant par la fusion de noyaux légers comme l'hydrogène
a lieu :
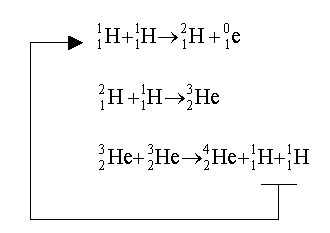
Ces réactions nucléaires
libèrent beaucoup d'énergie. La surface des étoiles
peut atteindre 5700 °C voire plus.
Dans des étoiles plus
massives que le Soleil, des températures encore plus élevées
permettent la fusion de noyaux plus lourds pouvant former par
fusion des noyaux comme ceux de carbone, d'oxygène ou
de fer.
3.4. La fusion contrôlée.
Le projet ITER : la fusion
magnétique contrôlée de l'avenir.
 Source : CEA
Source : CEA
Le but est de piéger
et maintenir à très haute température un
plasma. Ce plasma est confiné dans une boîte immatérielle
de forme torique créée par des champs magnétiques.
On parle alors de confinement magnétique.
Ensuite, de contrôler
des réactions nucléaires telle que :
Avec 300 litres d'eau de mer,
on pourrait fournir 1 gramme de deutérium . C'est-à-dire
que l'eau des océans permettrait, à elle seule,
de subvenir aux besoins mondiaux de l'humanité pendant,
environ, un milliard d'années.
1 gramme de tritium libère
la même énergie que 13,5 tonnes de pétrole.
(10 fois plus que la fission)
  Imprimer Imprimer
III. Bilan de masse et d'énergie
d'une réaction nucléaire.
|
Méthode pour effectuer un bilan
de masse et d'énergie :
- On calcule le défaut
de masse Dm
= mréactifs - mproduits
- Si Dm =
mréactifs - mproduits > 0 alors il y a libération
d'énergie.
- On calcule l'énergie libérée en appliquant
la relation d'équivalence E = Dmc2
On utilisera les conversions
d'unité les plus appropriées afin de réduire
les applications numériques.

Attention, dans le cas de l'utilisation
des énergies de liaison on calcule l'énergie libérée
en effectuant le calcul suivant
E = Eliaison
d'une libération
d'énergie - Eliaison
d'un apport d'énergie
Car :

Voir exemple de la fission |
1. Exemple
pour la radioactivité : Cas d'une désintégration
a.
La réaction étudiée
est 
Données : mRa =
225,9771 u mRn = 221,9704 u mHe = 4,0015
u
1 u = 931,5 MeV/c2
- Calcul de Dm = mréactifs - mproduits
= 225,9771 - (221,9704
+ 4,0015) = 5,200 x 10-3 u
- La conversion appropriée est 1 u = 931,5 MeV/c2
- On applique la relation d'équivalence E = Dmc2 alors E = 5,200
x 10-3 x 931,5 = 4,84 MeV
2. Exemple
pour la fission.
La réaction étudiée
est 
Données : El (235U)
= 1784 MeV El (94Sr) = 808 MeV El (140Xe)
= 1161 MeV
Calcul direct de l'énergie
libérée :
E = El (libération d'énergie)
- El (apport d'énergie)
E = [El (94Sr) + El (140Xe)
]- El (235U) = (808 + 1161) - 1784 = 185 MeV
3. Exemple
pour la fusion.
La réaction étudiée
est 
Données :
Réactifs m3H
= 5,0074 x 10-27 kg m2H = 3,3437
x 10-27 kg
Produits m4He = 6,6447 x 10-27kg mn
= 1,6750 x 10-27kg
- Calcul de Dm
Dm
= mréactifs - mproduits
Dm =
(5,0074 x 10-27+ 3,3437 x 10-27) - (6,6447
x 10-27+ 1,6750 x 10-27)
Dm =
3,1400 x 10-29 kg
- On applique la relation d'équivalence
E = Dmc2
E = 3,1400 x 10-29 x (3,0 x 108)2
= 2,8260 x 10-12 J
E =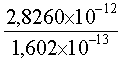 =
17,6 MeV =
17,6 MeV |